Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Může se norma zmenšit? (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 10. 2010 23:07
Může se norma zmenšit?
Zdravím kolegy,
tato otázka mi již několik dní vrtá hlavou:
Mějme "běžný" vektorový prostor  (
(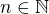 ) nad tělesem
) nad tělesem  , opatřený nějakou normou
, opatřený nějakou normou 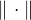 . Platí pro všechna
. Platí pro všechna 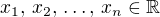 nerovnost
nerovnost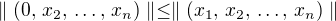 ?
?
Přijde mi, že všemožné verze trojúhelníkové nerovnosti o tom nic neříkají. Na druhou stranu, všechny "standardní" normy se tváří, že to splňují. Díky za jakékoliv postřehy! Nepotřebuji celé řešení, stačí snad i jen drobné naznačení.
Offline
- (téma jako vyřešené označil(a) Olin)
#2 15. 10. 2010 00:09
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Může se norma zmenšit?
↑ Olin:
Zdravím.
Pokusil jsem se najít normu, kde by to neplatilo. Velmi narychlo jsem si i dokázal, že to je skutečně norma (takže nevylučuju, že to nakonec nebude norma).
Offline
#3 15. 10. 2010 16:54
Re: Může se norma zmenšit?
Zdravím, díky moc za vyřešení. Trojúhelníkovou nerovnost se asi nikomu dokazovat nechce, tak aspoň takto:
Code:
In[2]:= Reduce[
ForAll[{a, b, c, d},
Sqrt[(a + b + c + d)^2/4 + (a - b + c - d)^2] <=
Sqrt[(a + b)^2/4 + (a - b)^2] +
Sqrt[(c + d)^2/4 + (c - d)^2]], {a, b, c, d}, Reals]
Out[2]= TrueOffline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Může se norma zmenšit? (TOTO TÉMA JE VYŘEŠENÉ)
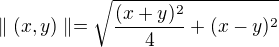

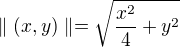 splňujeje trojúhelníkovou nerovnost. Vzhledem k tomu, že ta norma výše odpovídá pouze otočení os souřadnic o 45° (a asi i přeškálování), tak bych čekal, že to trojúhelníkovou nerovnost nepokazí.
splňujeje trojúhelníkovou nerovnost. Vzhledem k tomu, že ta norma výše odpovídá pouze otočení os souřadnic o 45° (a asi i přeškálování), tak bych čekal, že to trojúhelníkovou nerovnost nepokazí.