Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 10. 2010 14:54
Relace
Prosím o vyřešení těchto dvou příkladů. Jsou to poslední dva příklady z 15, které nemám ještě vyřešené a už fakt na to nemá sílu a mozek se mi zavařil někde u 11 příkladu :o(
1) Nechť R je reflexivní a tranzitivní relace na X. Dokažte, že  je ekvivalence na X.
je ekvivalence na X.
2) Dokažte nebo vyvraťte protipříkladem pro libovolné dvě relace R1,R2 na množině X:
Předem děkuju za jakoukoliv pomoc a ochotu
Offline
- (téma jako vyřešené označil(a) Majkl9102)
#2 18. 10. 2010 09:25
#4 18. 10. 2010 17:52
Re: Relace
U dvojky mi chybí nějaká definice těch funkcí fí, sigma a tau. Pro libovolné funkce asi by neplatilo nic.
Jednička:
Používám standardní zkratku 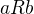 místo
místo 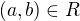 .
.
Uvědomění definice:  , tzn
, tzn 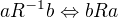 (bude použito často)
(bude použito často)
dále 
Důkaz symetrie:
Důkaz reflexivity: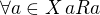 (R je reflexivní)
(R je reflexivní)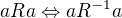

Důkaz tranzitivity:
Předpokládám  , chci získat
, chci získat 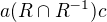

 (R je tranz.)
(R je tranz.) (R je tranz.)
(R je tranz.)
Relace 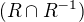 splňuje všechny vlastnosti ekvivalence.
splňuje všechny vlastnosti ekvivalence.
Offline