Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 19. 10. 2010 20:12
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Vzor množiny
↑ Fauſt:
Taková a,b však nemusí být jednoznačně určena. Budou však, je-li f (na daném intervalu) prostá.
"Máte úhel beta." "No to nemám."
Offline


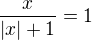 .
.![kopírovat do textarea $A = (1;2]$](/mathtex/5c/5c0ca7d33090bf9341d401e5f0e17ae6.gif) bude vzorem množiny množina
bude vzorem množiny množina  , takže řešíš soustavu (dvou) nerovnic
, takže řešíš soustavu (dvou) nerovnic