Matematické Fórum

NetFenix · 12. 04. 2008 10:35

Opět zdravím, tentokrát s problémem derivace, chtěl bych se zeptat, jestli je toto správné řešení když mám tedy:

Zadání: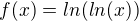
$f(x)=ln(ln(x))$
Řešení: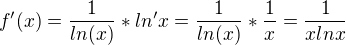
$f'(x)=\frac{1}{ln(x)}*ln'x=\frac{1}{ln(x)}*\frac{1}{x}=\frac{1}{xlnx}$

Je to správně??

A za druhé by mne zajímalo jak se dá řešit tento příklad: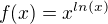
$f(x)=x^{ln(x)}$
Zkoušel jsem to vydolovat přes vzorec 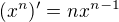$(x^n)'=nx^{n-1}$ , ale to asi nebude to pravé ořechové.

Díky za každou radu

Olin · 12. 04. 2008 10:41

To první je správně.

Druhé: buď pomocí logaritmického derivování (obě strany logaritmujeme a až pak derivujeme) nebo to upravíme jako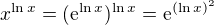
$x^{\ln x} = (\mathrm{e}^{\ln x})^{\ln x} = \mathrm{e}^{(\ln x)^2}$
což už se dá snadno derivovat.

Matematické Fórum

#1 12. 04. 2008 10:35

Deivace

#2 12. 04. 2008 10:41

Re: Deivace

Zápatí