Matematické Fórum

blanvan · 20. 10. 2010 19:49

Ahoj, potřebovala bych pomoct, jak dál.

Zadání je:
Vypočtěte první, druhou, třetí, až n-tou derivaci funkce a uveďte případná omezení pro x.
f(x) = e^x + e^-x
f(x)´= e^x - e^-x
f(x)´´= e^x + e^-x
f(x)´´´= e^x - e^-x

a teď nevim, jak tu n-tou... napadá mě jen f(x)^n = e^x +(-1)* e^-x

Pak bych se chtěla zeptat, jak je to s tim omezením pro x? Je to myšleno jako definiční obor? To by pak bylo x leží v R - {0}?

Děkuji moc za každou radu!!!

maly_kaja_hajnejch-Lazov · 20. 10. 2010 19:51

A proc nemuze byt x=0?

blanvan · 20. 10. 2010 20:18

Protože by pak žádná derivace nebyla? Nebo tam může být i ta 0?

teolog · 20. 10. 2010 20:27 — Editoval teolog (20. 10. 2010 20:28)

↑ blanvan:
Kdyby x bylo nula, tak lichá derivace derivace bude nula ( $e^0-e^0=1-1=0$ ) a sudá derivace bude dvě ( $e^0+e^0=1+1=0$ ). Takže nule nám rozhodně nevadí. Definiční obor funkce e^x je celé R (pro e^(-x) rovněž).

Co znamená ta hvězdička ve Vašem zápisu n-té derivace?

blanvan · 20. 10. 2010 20:43

Aha, tak děkuju za vyjasnění :) takže můžu chápat omezení pro x, že se po mně chce definiční obor?

Hvězdička značí násobení.

teolog · 20. 10. 2010 21:06

↑ blanvan:
V zásadě definiční obor plyne z omezení pro x. Jenže v tomto příkladě máte více než jednu funkci, dokonce jich je n. Takže místo definičního oboru pro každou fci je požadováno omezení pro x "globálně".

Jinak ten výsledek pro n-tou derivaci není dobře. Všimněte si, že u spočtených derivací se u druhého sčítance (e^(-x))střídá znaménko.
To Váš výsledek nedělá.

blanvan · 20. 10. 2010 21:19

A to omezení pro x globálně může být x leží v R? Nějak jsem se v tom zamotala..

To právě vidím, a proto nevim, jak mám tu n-tou derivaci zapsat, aby se mi tam to znaménko taky měnilo...

teolog · 20. 10. 2010 21:46

↑ blanvan:
V zadání je: uveďte případná omezení pro x. Takže bych odpověděl, x není nijak omezené.

K té mínus jedničce přidejte exponent n, tedy 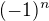$(-1)^n$ . U liché derivace tam bude mínus jedna, u sudé plus jedna.

blanvan · 21. 10. 2010 10:50

Já jsem si myslela, že to bude nějaká drobnost, co mi tam chybí, ale pořád jsem na to nemohla přijít..takže děkuji moc!!!!

Matematické Fórum

#1 20. 10. 2010 19:49

n-tá derivace

#2 20. 10. 2010 19:51

Re: n-tá derivace

#3 20. 10. 2010 20:18

Re: n-tá derivace

#4 20. 10. 2010 20:27 — Editoval teolog (20. 10. 2010 20:28)

Re: n-tá derivace

#5 20. 10. 2010 20:43

Re: n-tá derivace

#6 20. 10. 2010 21:06

Re: n-tá derivace

#7 20. 10. 2010 21:19

Re: n-tá derivace

#8 20. 10. 2010 21:46

Re: n-tá derivace

#9 21. 10. 2010 10:50

Re: n-tá derivace

Zápatí