Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 10. 2010 17:09
suradnice vrcholu
Zdravim, funkcia 
mam vypocitat suradnice vrcholu a priesecnikov s osami.
priesecniky vypocitat viem (vyriesim kvad. rovnicu)
ale neviem ako vypocitat vrchol, pokial sa tym mysli minimum alebo maximum funkcie.
Dakujem.
Offline
- (téma jako vyřešené označil(a) rimer)
#2 22. 10. 2010 17:17 — Editoval [ReD]mikl (22. 10. 2010 17:42)
Re: suradnice vrcholu
tím se myslí vrcholová rovnice, podle mého názoru
takže vytkneme mínus, dále doplníme vhodnou nulou (+4 a -4), protože nám to připomíná (x-2)na druhou a vyjde nám z toho - (x-2)na2 +3 = 0
takže souřadnice jsou V[2, 3], je "otočená" dolu (podle mínus před tím)
měl bych to mít dobře, ale samozřejmě kdyby ne, omlouvám se
EDITOVÁNO
Offline
#5 22. 10. 2010 17:53
Re: suradnice vrcholu
http://www.wolframalpha.com/input/?i=plot+-x^2%2B4x-1 mas to dobre :) prosim postup
Offline
#6 22. 10. 2010 17:59 — Editoval [ReD]mikl (22. 10. 2010 18:13)
Re: suradnice vrcholu
jo, tak V[2, 3] by mělo sedět
tady je návod http://www.sdilej.eu/pics/9366d8e1f0a8b … 575367.jpg AKORÁT JSEM PODĚLAL NULOVÝ BODY, KOUKNU NA NĚ ZNOVA
JE TO JASNÝ (MÁM BLBĚ DISKRIMINANT, BYLO MI TO DIVNÝ, ŽE BY PARABOLA BYLA TAK POZVOLNÁ) DISKRIMINANT JE 12 A NE 20
ještě něco málo k tý 4, nemusí to být samozřejmě vžycky 4, může to být i zlomek nebo jiné číslo
třeba když je rce xna2 +8x +5 = 0, tak tam doplníme 16, ale i odečteme
nebo xna2 +4x/3 +1, tak to je (x + 2/3)na2 - 4/9 +1 ... (x + 2/3)na2 +5/9
Offline
#8 22. 10. 2010 18:23 — Editoval LukasM (22. 10. 2010 18:24)
Re: suradnice vrcholu
↑ rimer:
Pokud už musíš počítat průsečíky s osou x, tak je výhodnější udělat nejdřív to, a potom si uvědomit jak vypadá graf kvadratické funkce. x-ová souřadnice vrcholu musí ležet přesně mezi těmi průsečíky, takže v našem případě opravdu vyjde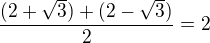 
. Ypsilonovou souřadnici vrcholu snadno spočítáme, když si uvědomíme, že vrchol leží na té parabole.
A nezapomeň ještě spočítat průsečík s osou y.
Offline