Matematické Fórum

RobbieMan · 25. 10. 2010 17:50

Zdravím,

potřeboval bych trochu s pomoci s tímto příkladem, jednoduše nemůžu přijít na způsob, jak každému součtu 2 až 12 přiřadit stejný počet možností , tak aby měli tu požadovanou stejnou pravděpodnost.

Děkuji za pomoc.

Olin · 25. 10. 2010 22:05 — Editoval Olin (25. 10. 2010 22:16)

Tak třeba lze postupovat takto: pokud je 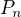$P_n$ pravděpodobnost, že na naší kostce padne $n$ , tak určitě musí platit
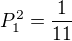$P_1^2 = \frac{1}{11}$ (součet 2 můžeme dostat pouze tak, že hodíme na obou jedničku)
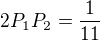$2 P_1 P_2 = \frac{1}{11}$ (součet 2 můžeme dostat zase jen tak, že na první kostce padne jednička a na druhé dvojka či naopak [proto 2x])
atd.
(EDIT: Opraveno 1/12 na 1/11)
Kdyby to šlo, tak nám na konci musí vyjít 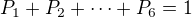$P_1 + P_2 + \dots + P_6 = 1$ .

(Teda doufám, že jsem pochopil zadání správně - mají se stranám kostky přiřadit takové pravděpodobnosti, aby při dvou hodech měl každý možný součet stejnou pravděpodobnost. Řečeno odborně, hledá se náhodné rozdělení na 1..6, jehož součet se sebou samým je rovnoměrné rozdělení.)

halogan · 25. 10. 2010 22:14

↑ RobbieMan:

Že bys byl ty ten přeběhlík z MFF na IES? Přesně tuto úlohu mám zítra v 8.00 odevzdávat jako domácí úkol, který bude obodovaný :-)

Jinak k postupu od ↑ Olin: není moc co dodat. Jen že na pravé straně rovnice má být 1/11. Do sporu se dostaneš při spočtení P_1, P_6, P_5, P_2 a P_3 (to už bude větší než 1).

Mnohem jednodušší důkaz je ale následující:

Jednoduše zjistíš, že 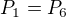$P_1 = P_6$ . Vezmeš si 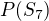$P(S_7)$ (pravděpodobnost součtu 7), což je 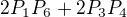$2P_1 P_6 + 2P_3P_4$ , což je ale 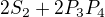$2S_2 + 2 P_3 P_4$ , což je spor s původním předpokladem, že se jednotlivé pravděpodobnosti součtů rovnají.

Hezký zbytek večera přeji.

Olin · 25. 10. 2010 22:20 — Editoval Olin (25. 10. 2010 22:23)

↑ halogan:
Zdravím, děkuji za upozornění na 1/11. Osobně jsem postupoval tak, že jsem si uvědomil rovnosti 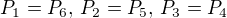$P_1 = P_6,\, P_2 = P_5,\, P_3 = P_4$ a pak jednoduše dopočítal 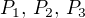$P_1,\, P_2,\, P_3$ z rovnic. A ejhle, 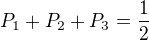$P_1 + P_2 + P_3 = \frac 12$ nevyšlo. Jde o krapet nechutná čísla, která bych na papíře spíše počítat nechtěl, ale přece sedím u komplu, ne? Každopádně tvůj důkaz je nesrovnatelně elegantnější.

halogan · 25. 10. 2010 22:59

↑ Olin:

Ta čísla opravdu jsou nepěkná. Já navíc replikoval situaci u písemky, takže jsem to počítal na papíře (pravda, nerovnost jsem poslal do Wolframu :-).

Jinak nebudu si ten jednodušší důkaz přivlastňovat, je to nápad spolužačky, ale moc se mi líbí.

RobbieMan · 26. 10. 2010 14:48

aha,já jsem neporozuměl zcela termínu "biased die", teď už to chápu

↑ halogan:
díky za oba důkazy, škoda, že jsem to ráno nestačil odevzdat

Matematické Fórum

#1 25. 10. 2010 17:50

Podmíněná pravděpodobnost

#2 25. 10. 2010 22:05 — Editoval Olin (25. 10. 2010 22:16)

Re: Podmíněná pravděpodobnost

#3 25. 10. 2010 22:14

Re: Podmíněná pravděpodobnost

#4 25. 10. 2010 22:20 — Editoval Olin (25. 10. 2010 22:23)

Re: Podmíněná pravděpodobnost

#5 25. 10. 2010 22:59

Re: Podmíněná pravděpodobnost

#6 26. 10. 2010 14:48

Re: Podmíněná pravděpodobnost

Zápatí