Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Vektory - 2 úlohy len z teoretického hľadiska (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 10. 2010 19:31
Vektory - 2 úlohy len z teoretického hľadiska
Robím úlohu a zároveň sa pripravujem na pisomku z matematiky (vektory)
1. mám všeobecnú rovnicu priamky p a mám určiť či je rovnobežná s priamkou, dannou dvomi bodmi...
(v tejto úlohe stačí zistiť smernicový vektor p zo všeobecnej rovnice a smernicový vektor AB? Potom overiť či je jeden smernicový vektor násobkom druhého?)
2. Zistite, či priamka p prechádza začiatkom sústavy súradníc.
Mám parametrické vyjadrenie 3 súradníc. Čo v tejto úlohe? Riešil som ju tak, že som z parametrickej vyjadril smerový vektor a bod A, no a dopočítal bod B, ten som dosadil do týchto 3 rovníc a zistil či sa t rovná rovnakému číslu v každej z nich.
Ďíky moc, naj ešte dnes, lebo zajtra píšem.. : )
Offline
- (téma jako vyřešené označil(a) ExSh00t)
#2 26. 10. 2010 19:39
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
1) Ano.
2) Stačí dosadit douřadnice daného bodu do rovnice přímky a zjistit, zdali platí rovnost. Pokud ano, daný bod leží na přímce.
Offline
#3 26. 10. 2010 20:01 — Editoval ExSh00t (26. 10. 2010 20:06)
Re: Vektory - 2 úlohy len z teoretického hľadiska
2. to som moc nepochopil (jedná sa o parametrické vyjadrenie, nepoznám t)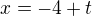
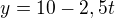
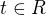
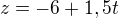
![kopírovat do textarea $A[-4; 10; -6]$](/mathtex/90/9050c3f09e35257647fbfc896a272f23.gif)
![kopírovat do textarea $B[-3; 7,5; -4,5]$](/mathtex/52/523c2c2fd68b6a09f88694d29e7ff7ef.gif)
![kopírovat do textarea $S (smernicovy vektor)[1; -2,5, 1,5]$](/mathtex/02/02917bde44b1f4fdd58b7f8c460d9e8a.gif)
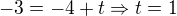


Takto som to urobil, je to správne? Najprv som rozmýšľal či nemôžem dosadiť priamo súradnice bodu A, ale tam potom vychádzajú samé nuly, dá sa to aj tak? Nakoniec som radčej cez smerový vektor odvodil súradnice B a tie dosadil. Potom overil či koeficient t je v každom vyjadrení rovnaký aby platili.
Offline
#4 26. 10. 2010 20:16
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Je to správně. Akorát trochu zbytečně zdlouhavé, mohl si už dosadit souřadnice bodu A nebo B a nepočítat směrnicový vektor, který si stejně nikde dál nepoužil.
Offline
#5 26. 10. 2010 20:29
Re: Vektory - 2 úlohy len z teoretického hľadiska
Práveže ja som súradnice nemal, len vyvodzoval opačne z parametrickej rovnice, najprv bod A a potom smerový vektor, jediné čo sa z toho dá a potom som nevedel, či tam mám dosadiť bod A, ktorý je v tých parametrických už zahrnutý. 
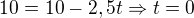
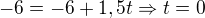
To mi nesedí, že ak vytiahnem z rovnice súradnice bodu, ktorý tam leží a dám ho tam ešte raz tak by to vychádzalo, vždy 0 nech je tam hoc koľko t, čo mi príde ako hlúposť mať súradnice bodu A v parametrických 2x. Preto som pomocou vzorca S = A - B ..vyjadril B a dosadil ten, inak neviem ako som to mal robiť.
Offline
#6 26. 10. 2010 20:36
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
To takhle, kouknul jsem se tak letmo a trochu špatně jsem pochopil, jak si to vlastně dělal. Každopádně to máš dobře a i tvoje úvodní úvaha je správná.
Offline
#7 26. 10. 2010 20:42 — Editoval ExSh00t (26. 10. 2010 20:51)
Re: Vektory - 2 úlohy len z teoretického hľadiska
Super, dík : )
Inak môže mi výjst pri parametrických vyjadreniach napr. u x, že sa mi tam stratí t a u y, t bude?
V jednom príklade mi totiž vylo: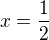

(jedná sa o os na úsečku)
A vlastne akú podmienku mám dať? 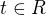 ? Os je vždy myslená priamka, či?
? Os je vždy myslená priamka, či?
Offline
#8 26. 10. 2010 21:00
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Pokud je jedna souřadnice směrnicového vektoru 0, tak parametr t tam nebude, respektive 0 * cokoli je 0, takže nemá cenu ho tam psát.
Offline
#9 26. 10. 2010 21:08
Re: Vektory - 2 úlohy len z teoretického hľadiska
4.3. Napíšte parametrické vyjadrenie a všeobecnú rovnicu osi úsečky AB, ak:![kopírovat do textarea $A[-4; 2]$](/mathtex/9a/9a579ac799fb26d3897363abb8510775.gif)
![kopírovat do textarea $B[5; 2]$](/mathtex/da/da95d9b9b3431e0801db02188452e5bd.gif)
-stred strany AB => bod ležiaci na osi ![kopírovat do textarea $S(AB) = [\frac12; 2]$](/mathtex/9b/9b55d10187c60a740f5e58c55c41c589.gif)
-smernicový vektor 
-normálový vektor => kolmý na smernicový 
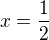
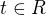

Takže takto by to bolo správne? Nie som si istý, či som správne použil ten normálový vektor a či os je priamka z R (úsečka a polpriamka to asi nebude)
Offline
#10 26. 10. 2010 21:21 — Editoval septolet (26. 10. 2010 21:21)
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Je to správně.
Normálový vektor přímky procházející body A a B je zároveň směrový vektor té osy. Směrový vektor a normálový vektor musejí být na sebe kolmé, takže se jejich skalární součin musí rovnat 0.
Offline
#11 26. 10. 2010 21:34 — Editoval ExSh00t (26. 10. 2010 21:43)
Re: Vektory - 2 úlohy len z teoretického hľadiska
Posledný typ úlohy : /
5.1. Zistite vzájomnú polohu priamok p, q, a ak sú rôznobežné, určte aj ich priesečník:
p: q: 

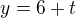
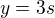
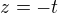
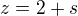
5.1 s týmto asi nepohnem + vôbec neviem akú vzájomnú polohu myslia, jedná sa len o vzorový príklad aby som vedel ako to riešiť, pamätám si to len matne, že nejako do rovnosti, cez sústavu, ale vypočítať to sám nezvládnem. Ak má niekto chuť a čas, moc mi pomôže doplniť poznatky. Ďakujem
Offline
#12 26. 10. 2010 21:45 — Editoval septolet (26. 10. 2010 21:45)
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Tohle bys už vyřešil:
Máš soustavu 3 rovnic o dvou neznámých.
Offline
#13 26. 10. 2010 21:56
Re: Vektory - 2 úlohy len z teoretického hľadiska
A čo tá poloha? Práve problém bol ten, že už si nepamätám tie sústavy, dlho dlho dlho som to nevidel. Ešte s tromi by som aj pohol ale 2 neznáme?
To si môžem vybrať z toho len 2 rovnice? veď z jednej rovnice si vyjadrím napr. s a dosadím do druhej a vypočítam t...načo tam je tretia? Potom to t kam? Dosadím do praametrickych rovnic priamky p a výjdu mi výpočty pre súradnice x,y, z? Tak by osm to robil.
Offline
#14 26. 10. 2010 21:59
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Přímky mohou být v prostoru totožné, rovnoběžné, různoběžné, nebo mimoběžné. Víš, jak to poznáš?
Ty rovnice mezi sebou můžeš sčítat, odčítat nebo třeba dosazovat. Třeba hned vidím, že když sečtu 2. a 3. rovnici, tak vypadne t. Dopočítáš s. Znova dosadíš a dopočítáš t.
Offline
#15 26. 10. 2010 22:09
Re: Vektory - 2 úlohy len z teoretického hľadiska
Možno by som si aj spomenul ale momentálne ma nenapadá nič ako zistiť z tých rovníc polohu...V zadaní mam že ak su rovnobežné nech určím priesečník, takže som mal zača polohou, teraz ani neviem či priesečník mám počítať...ak by som si určil smernicový vektor, dokážem určiť či sú rovnobežné podľa pravidla A = B . k ...totožné budú ak majú k 1 a A = vektoru B? Či sú rôznobežné alebo mimo neviem ako určiť.
s = 1
t = -3
čo teraz s tým? To mám dosadiť aj t aj s? ? Tým by som dostal u každej sústave parametrických rovníc priamky jeden bod o 3 súradniciach, teda 2 body.
Offline
#16 26. 10. 2010 22:27 — Editoval septolet (26. 10. 2010 22:27)
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Když dosadíme t a s třeba do 3. rovnice, tak vidíme, že to je rovnice, pravá strana se rovná té levé. Takže přímky jsou různoběžné, můžeme spočítat jejich průsečích. Stačí dosadit t do rovnice přímky p, případně s do rovnice přímky q a vyjdou nám souřadnice průsečíku těchto dvou přímek. Kontrolu lze provést tak, že souřadnice průsečíku dosadíme do druhé rovnice.
Jinak přímky v prostoru jsou totožné, když jejich směrové vektory jsou k-násobkem a zároveň libovolný bod jedné přímky leží i na druhé přímce.
Offline
#17 26. 10. 2010 22:41 — Editoval ExSh00t (26. 10. 2010 22:44)
Re: Vektory - 2 úlohy len z teoretického hľadiska
Fúha, takže postup je taký, že zistím smerové vektory (ak sú k násobkom sú rovnobežné, ak nie sú rovnobežné, sú rôznobežné alebo mimobežné) vypočítam t a s. Potom dosadím do jednej z rovníc a ak výjde pravda (rovnosť), sú rôznobežné ak by to nevyšlo sú mimobežné. Nakoniec som dosadil t a s a problém, je že mi u priamky p: (t) vyšlo: x = 11, y = 3, z = 3 a u q: (s) x = -1, y = 3, z = 3
Nemalo to výjsť rovnako? S tou totožnosťou predsa aj tak nemôžu byť totožné, lebo majú iné parametrické vyjadrenie či nie? Iba žeby bolo jedno vyjadrenie násobkom druhého.
Offline
#18 26. 10. 2010 23:03
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Dobře. Jde o to, že když sis vyjádřil t a s z 2. a 3. rovnice, tak bys měl ověřit rovnost u 1. rovnice. Tady to nevychází, takže přímky p a q jsou mimoběžné a průsečík nenajdeme. Prostě parametry t a s musí splňovat všechny 3 rovnice.
Offline
#19 26. 10. 2010 23:14
Re: Vektory - 2 úlohy len z teoretického hľadiska
Už to začínam chápať celkovo len neviem proste postup práce...keď mám zisťiť tú polohu, tak čím mám začať? Treba kontrolovať aj či sú rovnobežné? A totožné? Nedá sa to, že nie sú totožné vidieť hneď nejak? Myslím, že v tejto úlohe išlo o to či sú rôznobežné alebo mimobežné a ostatné nie je dôležité čo sa priesečníku týka.
Offline
#20 26. 10. 2010 23:24
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Nejprve si zjistíš, zdali jsou směrové vektory lineárně závislé. Pokud ano, jsou přímky buď rovnoběžné, nebo totožné. Pokud ne, pokračuješ viz postup výše (3 rce a řešíš tuto soustavu).
Offline
#21 26. 10. 2010 23:31
Re: Vektory - 2 úlohy len z teoretického hľadiska
A keď sú rovnobežné? Čo z toho vyplýva? Keď sú totožné, tak napíšem, že všetky riešenie pre p sú priesečníkom - platia i pre q. Inak teraz som sa ešte stretol s 2 rovnicami o 2 neznámych, tam ako zistím, či sú mimo alebo rôzno? Asi až keď budem konrolovať s a t pri p a q, podľa toho či mi to výjde rovnak?
Offline
#22 26. 10. 2010 23:38
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Rovnoběžné přímky nemají ani jeden společný bod. Totožné přímky mají společných nekonečně mnoho bodů.
Inak teraz som sa ešte stretol s 2 rovnicami o 2 neznámych, tam ako zistím, či sú mimo alebo rôzno? Asi až keď budem konrolovať s a t pri p a q, podľa toho či mi to výjde rovnak?
Ano. Ještě snad odkážu na nějaké ukázkové příklady s trochou teorie.
Offline
#23 27. 10. 2010 00:48
Re: Vektory - 2 úlohy len z teoretického hľadiska
Jasné, už temu rozumiem, problém bol v tom, že chodím na seminár, učiteľ nám dal riadnu haldu úloh, niektoré sme nikde nebrali. Inak uznávam ťa ako tomu rozumieš, ja po prebratí látky dostávam riadne výpadky...vždy viem poriadne len to čo sa učím.
Offline
#24 02. 11. 2010 11:23 — Editoval ExSh00t (02. 11. 2010 11:34)
Re: Vektory - 2 úlohy len z teoretického hľadiska
2. Zistite či priamka p prechádza začiatkom sústavy súradníc. (príklad na začiatku tohto topicu)
p:


Prvýkrát som to počítal, tak, že som si vyjadril smerový vektor z rovníc, vyjadril som si súradnice bodu A a dopočítal súradnice bodu B pomocou týchto 2 údajov, pretože dosaďovať súradnice bodu A do parametrických vyjadrení, ktoré ten bod A tvorí mi prišlo blbé, ten tam vždy bude patriť.
(LENŽE TOTO CELE MI TERAZ PRIPADA AKO BLBOSŤ!) Vôbec som asi nepochopil zadaniu, teraz keď na to pozerám, riešil by som to takto:
-začiatok sústavy súradníc - neznamená to náhodou, že x,y,z = 0 ??
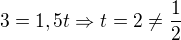
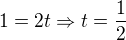
Z toho vyplýva, že neprechádza, v zadaní B) s inými parametrickými vyjadreniami inej priamky mi vyšlo aj že vychádza...poprosím ak máte čas analyzovať : )
Offline
#25 02. 11. 2010 11:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vektory - 2 úlohy len z teoretického hľadiska
↑ ExSh00t:
Zdravím,
sam si vytvařiš nepořádek v tématu - dle pravidel "jeden dotaz do jednoho tématu". Děkuji za pochopení.
Pokud prochází počátkem souřadnic, x, y, z jsou 0. Také mi vyšlo, že neprochází (kvůli poslednímu t).
Offline
Stránky: 1 2
- Hlavní strana
- » Střední škola
- » Vektory - 2 úlohy len z teoretického hľadiska (TOTO TÉMA JE VYŘEŠENÉ)
