Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 04. 2008 12:23
Půběh funkce - odmocnina
Ahojky lidi, tak jsem v kýblu s průběhem funkce, něco jsem zkusila, ale jistá si tím vůbec nejsem. Pomůžete? Děkuji. eja
y=\sqrt{x}+\frac{1}{\sqrt{x}}
1. Df: upravila jsem si na y=\sqrt{x}+\frac{1}{\sqrt{x}}=\sqrt{x}+\frac{\sqrt{x}}{{x}}=\frac{\sqrt{x}(1+x)}{{x}} a tedy x\ne0
a tedy dle \frac{1}{\sqrt{x}} musí být x\ge0, spojím-li obě podmínky, pak DF:(0,+\propto)
2. lichost, sudost, perioda - protože je Df platný pouze pro kladná čísla, nemá smysl uvažovat nad sudostí či lichostí a periodou
3. průsečíky s osami souřadnic
a) s osou x => y=0: \frac{\sqrt{x}(1+x)}{{x}}=0 upravíme \sqrt{x}(1+x)=0 a tedy buď se bude x=0 (což dle Df nejde) nebo x=-1 (také dle Df nejde) - s osou x se funkce neprotne
b) s osou y => x=0: \frac{\sqrt{x}(1+x)}{x}=y a \frac{\sqrt{0}(1+0)}{0}=y zde však jmenovatel nesmí být roven nule - s osou y se funkce také neprotne.
A jsme v kyblíku. Jestli to mám doposud správně, tak se asi teď mají dělat limity - spojitost funkce a tady jsem úplně v háji. Pěkně prosím, kdybyste mi rozepsali postup jako pro debily, bylo by to super. Děkuju moc, eja.
Offline
#2 14. 04. 2008 12:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Půběh funkce - odmocnina
↑ nika.v:
Zdravim, nedramatizuji to tak - prece ten zacatek jsi zvladla - tady jsem ho je dala do prehlednejsi podoby: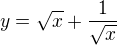
dalsi uprava ani nebyla tak nutna, ale pokud je to nazornejsi, tak proc ne - je OK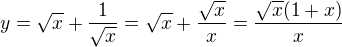
Df, sudost, lichost, pruseciky - nevidim zadny problem.
Limita - nez v bode nespojitosti, tak spis bych tomu rekla na okraji definicniho oboru - tedy k 0 zprava, a k +oo. Nemel by to byt problem.
Dal - v tematech VS na tomto foru je hodne odkazu na vypocty a na postupy (i vcetne odkazu na online vypocty) - http://mathonline.fme.vutbr.cz/Prubeh-f … fault.aspx
http://old.mendelu.cz/~marik/maw/index. … m=derivace (autorum stranek dekuji :-)
Pokracuj a pripadne se ozvi. Hodne zdaru :-)
Offline