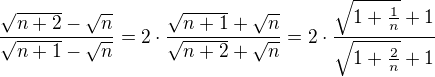Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)
#5 30. 10. 2010 14:12
- TriJindrich
- Zelenáč
- Příspěvky: 1
- Reputace: 0
Re: limita s odmocninou
No a co s tim citatelem, tam zustane nekonecno-nekonecno, to je na prd, ne ?
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)