Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 10. 2010 18:08
derivování
Dobrý večer,
mám příklad, který mám vypočítat a mám jej zařazený mezi derivacemi, ale ze zadání nechápu ani ťuk..
Zadání:
Součet dvou čísel je 12. Součin prvního s třetí odmocninou druhého je maximální. Najděte tato čísla.
Děkuji moc za každou radu!!! Mě při pohledu na to zadání nenapadá vůbec nic :(
Offline
- (téma jako vyřešené označil(a) Tychi)
#2 21. 10. 2010 18:16
Re: derivování
No máš dvě čísla, třeba 
, přičemž 
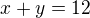. Teď chceš zjistit, kdy nabývá maximální hodnoty ![$x \sqrt[3]{y}$](/mathtex/bd/bd88596dd107b324970399bf09c38618.gif "kopírovat do textarea")
. Jde o funkci dvou proměnných, ale podle první podmínky to snadno převedeš na funkci jedné proměnné, jejíž extrém můžeš určit třeba derivováním.
Offline
#5 28. 10. 2010 10:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: derivování
↑ blanvan:
Zdravím,
dle postupu kolegy ↑ Olin: (děkuji) je vytvořena funkce ![$f(x, y)=x\sqrt[3]{y}$](/mathtex/d0/d07d3ca8651e636099a0aae8d937d66c.gif "kopírovat do textarea")
, kterou máme maximalizovat, kolega doporučuje převést na funkci jedné promenné tak, že z 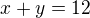vyjádříme 
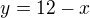a dosadíme do 
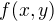místo y.
Nebo vyjádříme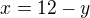 
a dosadíme do f(x, y) místo x, což bude pohodlnější na derivováví.
Potom máme funkci jedné promenné. Zvladneš to? Děkuji.
Offline
#6 31. 10. 2010 16:34
Re: derivování
Děkuji za radu, jen pak nevim, jak postupovat..
Vyjádřila jsem si tedy x a dosadila do funkce a potom zderivovala. Vyšlo mi y´= - [4* (x - 3)]/[3x^(2/3)]
Jen dál tápu.. chápu dobře, že musim najít extrémy funkce? Počítala jsem tedy takhle:
- [4* (x - 3)]/[3x^(2/3)] = 0
...z toho mi x vyšlo 3 a dosazením do původní rovnice jen dopočítám y = 9. Jen mám pocit, že je to moc lehké na to, aby to bylo správně :)
Offline
