Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dokažte morfismus algeber... (TOTO TÉMA JE VYŘEŠENÉ)
#2 31. 10. 2010 18:39
Re: Dokažte morfismus algeber...
Ty čtverečky a kolečka naznačují, že nejde o operace v kanonickém smyslu, ale o jinak definovanou verzi (zmodulenou, jak je definováno v zadání). Původní verze by na dané algebře nedávala smysl.
Abys mohl říct, že ![kopírovat do textarea $f: (X,\oplus,\odot)\rightarrow (Y,\boxed[2pt]{+},\boxed{\cdot})$](/mathtex/fa/fa77d37e1294ea2bf3348c7e005e6427.gif) je homomorfismus, tak potřebuješ ukázat:
je homomorfismus, tak potřebuješ ukázat:
1) 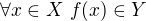
2) ![kopírovat do textarea $f(x\oplus y) = f(x)\boxed[2pt]{+} f(y)$](/mathtex/de/ded215f6a3ebd2775acebe47a2b57453.gif)
3) 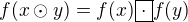
Takže:
1) je triviální
2) ![kopírovat do textarea $f(x\oplus y) = f((x+y)_{mod 6}) = ((x+y)_{mod 6})_{mod 3} = (x+y)_{mod 3} = (x_{mod 3} + y_{mod 3})_{mod 3} =\nl\quad = (f(x) + f(y))_{mod 3} = f(x)\boxed[2pt]{+} f(y)$](/mathtex/71/7156b22af8af659481587d5923078e40.gif)
3) obdobně jako 2)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dokažte morfismus algeber... (TOTO TÉMA JE VYŘEŠENÉ)
