Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Podle definice limity posloupnosti dokažte (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 11. 2010 22:27 — Editoval Keo (02. 11. 2010 23:12)
Podle definice limity posloupnosti dokažte
Offline
- (téma jako vyřešené označil(a) Keo)
#3 02. 11. 2010 23:42 — Editoval Keo (02. 11. 2010 23:43)
Re: Podle definice limity posloupnosti dokažte
No sem asi hodne natvrdly ale:
No.. a mam za ukol najit  takove, aby pro vsechna
takove, aby pro vsechna  platila nerovnost
platila nerovnost  pro kazde epsilon kladne... Mno a jak mam takove
pro kazde epsilon kladne... Mno a jak mam takove  v tomto pripade najit ?
v tomto pripade najit ?
nebo.. muzu za  vzit
vzit  ? (jak to udelali zde priklad 2.6)
? (jak to udelali zde priklad 2.6)
Offline
#4 03. 11. 2010 01:13
Re: Podle definice limity posloupnosti dokažte
↑ Keo:
Problém je v tom, že si si vzal príliš náročný príklad. Keďže nevieš dokazovať z definície, ukážem ti niečo ľahšie a potom vyriešim tento zložitejší.
Dokážem z definície, že 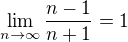
Ako píšeš, treba nájsť to  . Možno intuitívne vytušiť, že toto číslo bude závisieť od presnosti
. Možno intuitívne vytušiť, že toto číslo bude závisieť od presnosti  . Rozpíšem si to z definície, teda
. Rozpíšem si to z definície, teda
Požadujem, aby pre ľubovoľnú voľbu  platilo
platilo
no a to si vieme elementárnymi úpravami prepísať
Lenže číslo na pravej strane nerovnosti nemusí byť prirodzené pre nejakú voľbu  , preto si vezmeme najbližšie prirodzené číslo ako
, preto si vezmeme najbližšie prirodzené číslo ako 

Z uvedenej nerovnosti vyplýva, že bude splnená pre všetky n väčšie ako  . Napríklad presnosť e=0.01 bude splnená pre n väčšie ako
. Napríklad presnosť e=0.01 bude splnená pre n väčšie ako 
A skutočne, pretože 
NASPAT K ZADANIU
Mal by si si rozmyslieť, že ak nájdem to
 pre ten odhad, tak bude platiť aj pre pôvodnú postupnosť. Odhad si ešte o niečo vylepším, aby sa s ním dobre pracovalo
pre ten odhad, tak bude platiť aj pre pôvodnú postupnosť. Odhad si ešte o niečo vylepším, aby sa s ním dobre pracovalo
Požadujeme

Úpravami zo strednej školy dospejeme k nerovnici

Keďže
 je kladné, tak ide o konvexnú parabolu, čiže riešením dostaneme
je kladné, tak ide o konvexnú parabolu, čiže riešením dostaneme
a ako
 zvolíme
zvolíme
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Podle definice limity posloupnosti dokažte (TOTO TÉMA JE VYŘEŠENÉ)





