Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2008 19:07 — Editoval Boykins (16. 04. 2008 19:36)
Průběh funkce - dva příklady
Ahoj prosim vás, mohl by mi někdo poradit s těmito dvěma příklady? Jsem už z toho docela hotovej a u těchto dvou jsem se totálně zasekl.
http://img396.imageshack.us/my.php?imag … enicz3.jpg
potřeboval bych tam:
1. Definiční obor, jestli je funkce lichá nebo sudá
2. Body ve kterých není funkce definovaná, ale má v nich jednostranné limity, výpočet těchto limit, limity v nevlastních bodech, intervaly spojitosti
3. Průsečíky grafu funkce s osami x a y, znaménka funkčních hodnot
4. Výpočet 1.derivace, nulové body 1.derivace a body, ve kterých neexistuje 1.defivace
5. Lokální extrémy, intervaly monotonosti
6. Výpočet 2.derivace, nulové body 2.derivace a body, ve kterých neexistuje 2.derivace
7. Inflexní body, intervaly konvexnosti a konkávnosti
8. Asymptoty
9. Obor hodnot
10 Graf
ten graf bych už poté zvládnul případně
najde se někdo? :(
Offline
#2 16. 04. 2008 19:58
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Průběh funkce - dva příklady
racionalni funkce :)
to je jako stvorene pro MAW http://old.mendelu.cz/~marik/maw/index.php?form=prubeh
zkuste nejdriv ten odkaz a potom se pripadne poptavejte dal
Offline
#4 16. 04. 2008 21:21
Re: Průběh funkce - dva příklady
smernice je vpodstate tangens uhlu...
napr tan 90 nejni definovan... takze pokud budes mit asymptotu kolmou na x (rovnobeznou s y) tak muzes mit treba bez smernice...
obor hodnot si urcis z kroku co udelas predtim... zjistis kdy je rostouci klesajici, minima a maxima, a z toho uz to krasne urcis . . .
Offline
#5 16. 04. 2008 21:59
Re: Průběh funkce - dva příklady
↑ liquid:
Nejsem si jista, zda obor hodnot lze urcit pomoci vypoceni maxima a minima....asi mluvis o lokalnich extremech? Nepletu se?
To, ze ma funkce lokalni minimum a lokalni maximum neznamena, ze oborem hodnot je vse mezi temito hodnotami...aspon ne obecne u vsech funkci.
Nejlepe se obor hodnot stanovi jako definicni obor inverzni funkce, ale je fakt, ze po me nikdy nikdo obor hodnot pri urceni prubehu fce nechtel. vetsinou jsme ho urcovali az na zaklade znalosti grafu.
Offline
#7 16. 04. 2008 22:07 — Editoval Jorica (16. 04. 2008 22:25)
Re: Průběh funkce - dva příklady
↑ Boykins:
Asymptota je obecne primka, ke ktere se graf funkce blizi, ale nikdy se ji nedotkne.
Ty bez smernice hledame v bodech, kde funkce neni definovana nebo v krajnich bodech definicniho oboru. Asymptoty bez smernice jsou pak kolmice na osu x (Pr. fce ln x pro x=0, tg x pro x=Pi/2, ...) Proto pokud vime, ze fce ma jako definicni obor vsechna realna cisla, pak nemame kde hledat asymptoty bez smernice a ty neexistuji.
Asymptoty se smernici jsou pak takove primky, ktere maji konkretni smernici, tj. sviraji s osou x nejaky uhel (krome praveho).
Pr. fce 1/x ma pro x=0 asymptotu bez smernice (je ji osa y, tj. primka o rovnici x=0) a soucasne se graf fce 1/x pro x jdouci k nekonecnu blizi k ose x (totez pro x jdouci k -nekonecnu), tzn. osa x (promka s rovnici y=0) je asymptotou se smernici.
Offline
#8 16. 04. 2008 22:12
Re: Průběh funkce - dva příklady
↑ liquid:
jo, tve uvaze rozumim, ale nedokazu posoudit, zda obecne funguje u "obtiznejsich" funkci. Kazdopadne by bylo nutne uvazit i asymptoty, prip. hodnoty limit v nevlastnich bodech (nekonecno, -nekonecno) a bodech nespojitosti, protoze funkce muze klesat, ale to, jestli klesa az do -nekonecna nebo se blizi k nejake hodnote, to z hodnot lokalnich extremu a toho, zda funkce roste ci klesa neurcim...chce to vyhodnotit vice udaju.
Offline
#11 16. 04. 2008 23:01 — Editoval Jorica (16. 04. 2008 23:10)
Re: Průběh funkce - dva příklady
↑ Boykins:
jo, ty asymptoty bez smernice mas stanovene dobre.
Ktere limity mas na mysli...ty z bodu 2?
Jinak obe fce maji jako obor hodnot vsechna realna cisla. To je napriklad mozne odvodit z vypoctu MAW (a overit si to podle grafu, ktere ti to taky "vyplivlo" ;-)) Ale jak jsme se tu uz "dohadovali", na ten obor hodnot musis posoudit vice udaju.
Offline
#12 16. 04. 2008 23:34 — Editoval Jorica (16. 04. 2008 23:36)
Re: Průběh funkce - dva příklady
No zkusim ti neco natukat, ale predem se omlouvam, s TEXem se tu potykam teprve druhy den ;-)
Fce 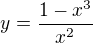 ma
ma 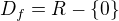 , takze hledas jednostranne limity pro
, takze hledas jednostranne limity pro  a
a 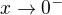 ..to uz jsi ale pocital u tech asymptot bez smernice..obe ti vysly
..to uz jsi ale pocital u tech asymptot bez smernice..obe ti vysly  .
.
Limity v nevlastnich bodech jsou limity pro 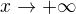 a
a 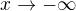 .
. 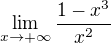 vypoctes pomoci L'Hosp. pravidla a vyjde ti
vypoctes pomoci L'Hosp. pravidla a vyjde ti 
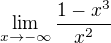 vypoctes obdobne a vyjde ti
vypoctes obdobne a vyjde ti  .
.
Fce neni spojita v bode  , na intervalech
, na intervalech 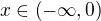 a
a 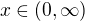 je spojita. Z vypoctu vyse uz vis, ze pro:
je spojita. Z vypoctu vyse uz vis, ze pro: jde graf fce do
jde graf fce do  a
a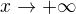 klesá graf k
klesá graf k  . protoze je fce na intervalu
. protoze je fce na intervalu 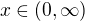 spojita, nabyva vsech hodnot mezi
spojita, nabyva vsech hodnot mezi  a
a  , takze oborem hodnot jsou vsechny R-cisla.
, takze oborem hodnot jsou vsechny R-cisla.
Offline
