Matematické Fórum

vysoka · 08. 11. 2010 22:10

$\lim_{n\to\infty}\frac1{5^n}$ $2n \choose n$

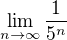
takze to kombinacne cislo vycislimi podla vztahu ... (2n!)/((2n-n)!n!)
ale vsak ten clen s faktorialmi bude vacsi ako ta exponenciala , ze ?
ale aj tak to vypada ze to pravdepodobne ide k nule podla prveho podielu 1 a exponencialnej FCiE Dakujem

vysoka · 08. 11. 2010 22:27

no v menovateli sa vyrusia n!

vysoka · 08. 11. 2010 22:32

mozne odpovede
4/5
5/4
0
1
nekonecno
neexistuje

vysoka · 08. 11. 2010 22:37

prvy aj druhy clen po dosadeni dostatocne velkeho n . ka idu k 0 ...

mancini · 08. 11. 2010 22:59

kua sorry!!!! mystifikace nejvetsi ... s tim faktorialem zapomen na to, co jsem napsal :-)

mancini · 08. 11. 2010 23:11

za to, ze jsem takovej mamlas ...

$\lim_{x\rightarrow{\inft}}\frac{1}{5^n}{2n\choose{n}}=\lim_{x\rightarrow{\inft}}\frac{1}{5^n}{\frac{2n!}{(2n-n)!n!}=\lim_{x\rightarrow{\inft}}\frac{1}{5^n}{\frac{(n+1)(n+2)...(2n)}{n!}}$

a dal uz je to easy, ne?

vysoka · 08. 11. 2010 23:32

ano vysledok je NULA :)

mancini · 08. 11. 2010 23:55

jj ;-)

Matematické Fórum

#1 08. 11. 2010 22:10

limita s kombinacnym cislom

#2 08. 11. 2010 22:27

Re: limita s kombinacnym cislom

#3 08. 11. 2010 22:32

Re: limita s kombinacnym cislom

#4 08. 11. 2010 22:37

Re: limita s kombinacnym cislom

#5 08. 11. 2010 22:59

Re: limita s kombinacnym cislom

#6 08. 11. 2010 23:11

Re: limita s kombinacnym cislom

#7 08. 11. 2010 23:32

Re: limita s kombinacnym cislom

#8 08. 11. 2010 23:55

Re: limita s kombinacnym cislom

Zápatí