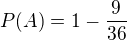Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2008 19:31 — Editoval liquid (16. 04. 2008 20:01)
lehka pravdepodobnost
Ahoj..
jaka je pravdepodobnost, ze na dvouch hracich kostkach padne alespon jedno lichy cislo?
diky za pomoc
dostanu se k vysledku 3/4
to zas jo...
ale jen tak ze celkem pracne zjistim kolik je moznych kombinaci s lichym cislem...
jak byste postupovali co nejefektivnejs vy?
Offline
#4 16. 04. 2008 20:15
Re: lehka pravdepodobnost
A nebo jeste jednoduseji:
Pravdepodobnost, ze na prvni kostce padne sude = 1/2, to same pro druhou. Takze pravdepodobnost, ze sude padne na obou je 1/2*1/2 = 1/4, cili pravdepodobnost opacneho jevu je 1-1/4.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#5 16. 04. 2008 20:17
#7 16. 04. 2008 20:37
Re: lehka pravdepodobnost
↑ Ginco:
To prvni reseni jsem asi nejak omylem preskocil a precetl si rovnou to tvoje. Omlouvam se za redundantni informaci.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#8 16. 04. 2008 20:41
Re: lehka pravdepodobnost
diky vam !
jen me proste nejde dohlavy jaky je rozdil pri hodu 2ma kostkama oproti hodu 2x jednou kostkou...
jedno se pocita tak ze tam je rozdil mezi 3a1 a 1a3 ale v druhem se to proste bere jen jakoze padla 3ka a jednicka...
obracene bych to jaks taks chapal, ale moznost ze 1_3 a 3_1 jsou ruzne hody plati pro to, kdyz hazim obouma najednou :( coz mi prave prijde divny
Offline
#9 16. 04. 2008 21:11
Re: lehka pravdepodobnost
Aha, uz asi chapu cemu nerozumis. Je to rozdil mezi kombinatorikou a prevdepodobnosti.
Chci napriklad spocitat, kolik moznosti mam, kdyz hazim dvem kostkami. Pokud mi zalezi na poradi, tedy "1 a pak 3" je neco jineho nez "3 a pak 1". Tady musim hazet postupne, protoze kdyz hodim dvema kostkami najednou, nepoznam, ktera byla ta prvni a ktera druha. Tady mam potom 36 ruznych moznosti.
Pokud mi nezalezi na poradi, cili dulezite je pro me, ze padla jednicka a trojka, lhostejno v jakem poradi, tak je jedno zda hazim kostkami najednou nebo postupne. Potom mam moznosti pouze 21 (zkus si to spocitat).
Pokud ale pocitam pravdepodobnost, tak si vzdy musim zvolit nejaky matematicky model situace. My jsme si zvolili model, kdy nam zalezi na poradi. Tedy nasim prostorem jevu je mnozina usporadanych dvojic cisel. Kazda dvojice predstavuje jeden mozny hod kostkou. Tento model ma jednu obrovskou vyhodu. Vsechny jevy (hody kostkou), jsou stejne pradepodobne. Takze nam staci prijit na to, kolik z tech jevu je pro nas priznivych a spocitat, jak velkou cast cele te mnoziny moznych jevu vlastne ty priznive jevy tvori. To spocitame velmi snadno, jak uz tady bylo stokrat receno.
Nyni zkusme zvolit jiny model situace. Ted nam nebude zalezet na poradi. CIli nase mnozina moznych jevu bude mensi. Bude mit jenom 21 prvku misto 36. Tady je ale problem. Jev ze padnou dve ruzna cisla ma vetsi pravdepodobnost, nez ze padnou dve stejna! Jednicku a dvojku totiz muzu hodit dvema zpusoby (1 a 2 nebo 2 a 1) zato dve sestky jenom jednim. Dve sestky maji pravdepodobnost 1/36, zato jev {1, 2} ma pravdepodobnost 1/18. Kdybychom secetli pravdepodobnosti vsech jevu, ktere jsou pro nas priznive, taky bychom nakonec dostali 3/4. Bylo by to ale pracnejsi. Proto se nam vic hodil ten prvni model.
Cili pri pocitani pravdepodobnosti je v podstate jedno, zda nam zalezi nebo nezalezi na poradi kostek, ale v prvnim z tech pripadu se to bude lip pocitat.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline