#1 13. 11. 2010 17:59
Výpočet limity
Ahoj, mám problém s následující limitou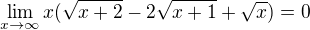
udělala jsem si graf a vidím z něj, že jde k nule
když se ji ale snažím počítat, nevychází mi to. Zkoušela jsem výraz rozšířit, ale nedostala jsem se ke kloudnému výsledku.
Mohl by mi někdo, prosím, pomoct?
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
- (téma jako vyřešené označil(a) Esperance)
![$\lim_{x\to\infty}x(\sqrt{x+2}-2\sqrt{x+1}+\sqrt{x})=\lim_{x\to\infty}x\(\frac{1}{\sqrt{x+2}+\sqrt{x+1}}-\frac{1}{\sqrt{x+1}+\sqrt{x}}\) = \nl\lim_{x\to\infty}x\cdot\[\frac{\sqrt{x+1}+\sqrt{x}-\sqrt{x+2}-\sqrt{x+1}}{\(\sqrt{x+2}+\sqrt{x+1}\)\cdot\(\sqrt{x+1}+\sqrt{x}\)}\]= \lim_{x\to\infty}\frac{\sqrt{x}-\sqrt{x+2}}{\(\sqrt{1+\frac{2}{x}}+\sqrt{1+\frac{1}{x}}\)\cdot\(\sqrt{1+\frac{1}{x}}+\sqrt{\frac{1}{x}}\)}=0$](/mathtex/64/64cbc18a67ff7dd56e0ddeb04b746bda.gif "kopírovat do textarea")