Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 11. 2010 17:02
průběh funkce
Ahoj, potřebovala bych pomoci ještě s tímto příkladem, snad už posledním :) Já jsem se o něco pokoušela, ale vůbec si nejsem jistá u tohoto typu funkce..
Zadání:
f(x) = e^ (1/x)
1.Definičním oborem jsou všechna reálná čísla.
2.Průsečíky: s osou x = 0
s osou y = 0
3.Sudá/lichá - f(x) = e^ (1/x) = + nekonečno
f(-x) = e^ (-1/x) = + nekonečno funkce je sudá
4.Limity v +,-nekonečnu = 1
5.Monotónnost:
y´= - {[e^ (1/x)]/(x^2)}
Funkce je klesající v (-nekonečno,0) i v (0, + nekonečno)
V bodě x = 0 je lokální minimum
6. Konvexní, konkávní:
y´´= [(2x+1)* e^ (1/x)]/x^4
V intervalu (-nekonečno, -1/2) je funkce konkávní a v intervalu (-1/2, +nekonečno) je konvexní. Bod -1/2 je inflexní bod.
7. Asymptoty:
bez směrnice nejsou
se směrnicí: y = kx + q
k = lim e^ (1/x) = nekonečno ... q není třeba počítat - neexistuje ani asymptota se směrnicí.
Byla bych ráda, kdyby jste mi to někdo zkoukl a napsal, co mám třeba špatně - doufám, že ne všech 7 bodů :)
Děkuji moc!!!
Offline
- (téma jako vyřešené označil(a) blanvan)
#2 09. 11. 2010 20:19
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: průběh funkce
↑ blanvan:
1. Vzhledem k tomu, že x je ve jmenovateli, tak definiční obor nejsou všechna reálná čísla.
2. Průsečíky s osami neexistují. (e na cokoliv kromě nuly nemůže být nula).
3. Jak souvisí sudost a lichost funkce s nekonečnem? Nechápu uvedený postup.
4. Limity: ta jednička je dobře, ale ještě by to chtělo napsat, zda je shora nebo zdola. A navíc chybí limita v bodě, který by měl vyplynout z definičního oboru (správého!)
5. Derivace je dobře, s tím minimem to není tak jednoduché.
Ostatní nechám na později nebo kolegům, musím běžet.
Offline
#3 10. 11. 2010 11:24
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: průběh funkce
kolik je limita v nule? Presneji, kolik jsou jednostranne limity v nule? Jedna by mela utact do nekonecna. Takze svisla asymptota je
Kolik je limita v nekonecnu? A kolik v minus nekonecnu? Mely by byt konecne, takze je dokonce vodorovna asymptota (s nulovou smernici).
k = lim e^ (1/x) = nekonečno -- neni pravda ani ze se takto vypocita k, ani ze ta limita je nekonecno
Offline
#4 15. 11. 2010 13:45
Re: průběh funkce
Děkuji za rady :) pro přehled jsem funkci s mým postupem znovu zkopírovala a trochu poopravila podle Vašich rad, ale budu ráda, když mi n a to ještě juknete, protože typ téhle funkce je pro mě španělská vesnice.
Zadání: f(x) = e^ (1/x)
1.Definičním oborem jsou všechna reálná čísla - {0}
2.Průsečíky: s osou x a y neexistují
3.Sudá/lichá - f(x) = e^ (1/x) = 1
f(-x) = e^ (-1/x) = 1 funkce je sudá S tou sudostí a lichostí si moc rady nevim, ve skriptech o tom moc zmínka není, ale co jsem se dívala, v průběhu by být měla, jen pořádně nevim, jak na to.
4.Limity v +,-nekonečnu = 1 omezená zdola? Omezenost jsem u limit nikdy nepočítala, tak nevim.
Limita pro 0- = 0
Limita pro 0+ = nekonečnu
5.Monotónnost:
y´= - {[e^ (1/x)]/(x^2)}
Funkce je klesající v (-nekonečno,0) i v (0, + nekonečno)
V bodě x = 0 je funkce nespojitá, proto v ní extrém neexistuje.
6. Konvexní, konkávní:
y´´= [(2x+1)* e^ (1/x)]/x^4
V intervalu (-nekonečno, -1/2) je funkce konkávní a v intervalu (-1/2, +nekonečno) je konvexní. Bod -1/2 je inflexní bod.
7. Asymptoty:
bez směrnice vzhledem k def.oboru jsou:
Limita pro 0+ = nekonečnu
Asymptota bez směrnice je v bodě x = 0
se směrnicí: y = kx + q
k = lim e^ (1/x) /x = 0 pro +,- nekonečno
q = lim e^ (1/x) = 1 pro +,- nekonečno asymptota se směrnicí y = 1
Vypadá tento postup už trochu lépe než ten předešlý? :) Děkuji za každou radu!!!
Offline
#5 15. 11. 2010 14:53 — Editoval Rumburak (15. 11. 2010 15:13)
Re: průběh funkce
↑ blanvan:
Zadání: f(x) = e^ (1/x)
1.Definičním oborem jsou všechna reálná čísla - {0}
SPRÁVNĚ
2.Průsečíky: s osou x a y neexistují
SPRÁVNĚ
3.Sudá/lichá - f(x) = e^ (1/x) = 1
f(-x) = e^ (-1/x) = 1 funkce je sudá S tou sudostí a lichostí si moc rady nevim, ve skriptech o tom moc zmínka není, ale co jsem se dívala, v průběhu by být měla, jen pořádně nevim, jak na to.
ŠPATNĚ. Je vidět, že opravdu nevíš, o co jde. Připomeňme si definice :
Funkce f je lichá, právě když pro každé 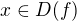 je též
je též 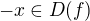 a zároveň
a zároveň  .
.
Funkce f je sudá, právě když pro každé 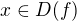 je též
je též 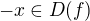 a zároveň
a zároveň  .
.
4.Limity v +,-nekonečnu = 1 SPRÁVNĚ
omezená zdola? Omezenost jsem u limit nikdy nepočítala, tak nevim.
Limita pro 0- = 0 SPRÁVNĚ
Limita pro 0+ = nekonečnu SPRÁVNĚ
Funkce f je zdola omezená na celém D(f) (všechny funkční hodnoty jsou větší než 0),
na intervalu (-oo, 0) je omezená i shora (její fukční hodnoty jsou tam menší než 1),
na intervalu (0, +oo) shora omezená není, protože v nule zprava má limitu +oo.
5.Monotónnost:
y´= - {[e^ (1/x)]/(x^2)}
Funkce je klesající v (-nekonečno,0) i v (0, + nekonečno) SPRÁVNĚ
V bodě x = 0 je funkce nespojitá, proto v ní extrém neexistuje.
ŠPATNÉ zdůvodnění. O extrému v bodě x = 0 nelze mluvit, protože v něm funkce není definována.
6. Konvexní, konkávní:
y´´= [(2x+1)* e^ (1/x)]/x^4 SPRÁVNĚ
V intervalu (-nekonečno, -1/2) je funkce konkávní SPRÁVNĚ
a v intervalu (-1/2, +nekonečno) je konvexní. ŠPATNĚ - v bodě 0, kde funkce není definována, se to pokazí.
Fce je konvexní pouze na každém z intervalů (-1/2, 0), (0, +oo).
Bod -1/2 je inflexní bod. SPRÁVNĚ
7. Asymptoty:
bez směrnice vzhledem k def.oboru jsou:
Limita pro 0+ = nekonečnu
Asymptota bez směrnice je v bodě x = 0 SPRÁVNĚ ... a rovnici má x = 0 .
se směrnicí: y = kx + q
k = lim e^ (1/x) /x = 0 pro +,- nekonečno
q = lim e^ (1/x) = 1 pro +,- nekonečno asymptota se směrnicí: y = 1 SPRÁVNĚ
POZN. V písemce nebo u zkoušky je pak potřeba dbát i na formální stránku zápisu - v tomto ohledu poněkud pokulhává
zejména bod 4 - věřím, že tužkou na papíře by to bylo zapsáno lépe.
Offline
#6 15. 11. 2010 15:08
Re: průběh funkce
Děkuji moc!!! Když je to takhle hezky vypsané v tom mém postupu, tak to lépe chápu!
K těm bodům, co jsem měla špatně:
3. Už to chápu :) funkce je lichá
5. U tohoto zdůvodnění jsem měla na mysli, že pokud se podívám na graf, jako lok.minimum mi tam vychází x=0, ale funkce není v tomto bodě definována..takže lok. extrémy funkce nemá? A globální?
Offline
#7 15. 11. 2010 15:29
Re: průběh funkce
↑ blanvan:
Ad 3. Daná funkce NENÍ lichá ANI sudá. Geometricky tyto pojmy znamenají:
Sudá funkce je taková, jejíž graf je osově souměrný dle souřadnicové osy y.
Lichá funkce je taková, jejíž graf je středově souměrný dle počátku soustavy souřadnic.
Nic takového zde nenastává. Stačí ZDE porovnat jednostranné limity v 0 : u sudé funkce by se musely shodovat,
u liché funkce by se pouze musely lišit znaménkem.
Ad 5. Když funkce nemá lokální extrémy, nemá ani globální (protože glob. extrém je zároveň lokálním extrémem).
Funkce má supremum (což je +oo ... ta limita v 0+) a infumum (což je 0 ... limita v 0-) , ale žádné z těchto hodnot nenabývá.
Offline