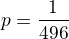Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 11. 2010 18:39
Pravdepodobnost
Znenie ulohy:
vypocitajte aka je pravdebodobnost ze vyhram v lotte ak podam jeden tiket:
dokopy je tam 49 cisel, a nato aby som vyhral potrebujem uhadnut 6 vylosovanych cisel.
MOje riesenie je:
P= pocet priaznivych udalosti/pocet vsetkych udalosti
POcet priaznivych udalosti =49!/(49-6)!*6! =13983816
POcet vsetkych udalosti= 49*48*47*46*45*44
cize P=0.0138%
pocital som to dobre? nie som si isty ci som dobre vypocital pocet vsetkych udalosti, ale pocet priaznivych udalosti by malo byt spravne, si myslim.
Offline
- (téma jako vyřešené označil(a) faktorial)
#2 16. 11. 2010 10:29
Re: Pravdepodobnost
↑ faktorial:
To nemáš dobře.
Budeme spolu uvažovat.
Taháme 6 čísel a je jedno jestli vytáhneme nejdříve např. 1 a potom např, 5 nebo naopak. Z toho tedy vyplývá, že děláme skupiny po 6-ti prvcích (z 49) kde nezáleží na pořadí. Tomu odpovídají kombinace 6-té třídy z 49 prvků. To jsou všechny možné případy. Mimochodem tomu odpovídá to tvoje první číslo.
A teď kardinální otázka. Kolik je možností, že budou vytažena právě ta čísla, když nezáleží na pořadí v jakém je taháme. No přece pouze jedna jediná.
Takže pravděpodobnost, že vyhrajeme je převrácená hodnota čísla 13983816.
Offline