Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Kombinatorika zadani č.1 (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 11. 2010 08:17
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Kombinatorika zadani č.1
Kombinatorika
Dokažte, že existuje číslo tvaru 20102010...2010, které je dělitelné 1111.
Návod: Každé číslo tvaru 20102010...2010 lze zapsat jako 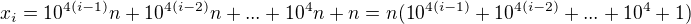 , pokud n=2010. Součet v závorce se dá pěkně vyjádřit. Pak volte i=1, 2, ..., 1112 a ukažte pomocí Dirichletova principu, že vždy existují
, pokud n=2010. Součet v závorce se dá pěkně vyjádřit. Pak volte i=1, 2, ..., 1112 a ukažte pomocí Dirichletova principu, že vždy existují  , taková, že číslo
, taková, že číslo 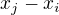 je dělitelné 1111.
je dělitelné 1111.
-----------------------------------------------------
Pokud jsem to správně pochopil, tak mám dokázat, že třeba 20102010-2010 je dělitelné 1111 nebo 201020102010201020102010-201020102010 je dělitelné 1111.
Pokud taky správně předpokládám, že chceme dělitelnost bezezbytku tak je možné, že te ani nedokážu, protože je možné, že dělitelné není?
Ať jsem to zkoušel vydělit na kalkulačce nebo v excelu tak se můžu stavět na hlavu ale nikdy mi nevyjde číslo bez desetinné části.
Potřeboval bych poradit jak na to jestli dělitelné opravdu je.
Offline
- (téma jako vyřešené označil(a) mysteriouss)
#2 11. 11. 2010 08:35
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kombinatorika zadani č.1
↑ mysteriouss:
Pomocí Dirichletova principu máš ukázat, že existují  taková, že číslo
taková, že číslo 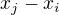 je dělitelné 1111.
je dělitelné 1111.
Offline
#3 11. 11. 2010 08:42
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
no to ano, ale ja uvazuji ze jelikoz  tak ze napr
tak ze napr 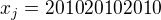 a
a 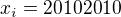 tj.
tj. 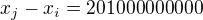 a vyjde mi
a vyjde mi 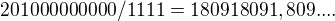
pomoci toho Dirichletova principu to bude vycházet jinak? Díval jsem se na internetu a moc mi ten dirichlet neříká snad jen že jsem se dočetl že všude na zemi se tomu říká jinak.
Offline
#4 11. 11. 2010 08:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kombinatorika zadani č.1
↑ mysteriouss:
Zkus si pro začátek tohle: Pomocí Dirichletova principu ukažte, že mezi dvaceti různými přirozenými čísly existují dvě různá čísla, která mají stejnou poslední cifru.
Offline
#5 15. 11. 2010 00:13
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
K tomu co jsi napsal, že si mám zkusit tak podle toho co jsem se všude na internetu dozvěděl ohledně Dirichletova principu, tak nikde se nic nepočítá, všude se jen teoreticky dokazuje ... tak k tomu s 20 čísly bych jako výsledek dal asi tohle:
mám 20 různých čísel, mám 10 různých možností aby byla poslední cifra jiná, z čehož mi vychází, že vždy budou minimálně dvě různá čísla, která budou mít stejnou poslední cifru.
Je to takhle správně? Nebo by ta odpověď měla být jiná?
Offline
#6 15. 11. 2010 00:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kombinatorika zadani č.1
↑ mysteriouss:
Jo, to je dobře. Takže jsi ukázal, že taková dvě čísla existují. Přesto když si nějaká dvě z dvaceti vyberu, tak můžou mít různou poslední cifru. Vidíš tu podobnost s úlohou, kterou máš řešit? Ty sis vybral nějaká dvě  , ale tvrzení pro ně neplatí. To ale neznamená, že neexistují jiná, pro která tvrzení platí. A ty máš pomocí Dirichletova principu ukázat, že existují (podobně jako jsi to teď udělal v té návodné úloze).
, ale tvrzení pro ně neplatí. To ale neznamená, že neexistují jiná, pro která tvrzení platí. A ty máš pomocí Dirichletova principu ukázat, že existují (podobně jako jsi to teď udělal v té návodné úloze).
Offline
#7 15. 11. 2010 00:43
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
No a tady je právě ten problém, že tu podobnost nevidím jelikož v zadání je tolik čísel, že jsem z toho zmatený. :(
Offline
#8 15. 11. 2010 00:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kombinatorika zadani č.1
Možná nemusí být jasné, jakou úlohu hraje j v poslední části zadání „Pak volte…“. Dalo by se to přeformulovat takto:
„Pomocí Dirichletova principu ukažte, že existují  taková, že číslo
taková, že číslo 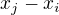 je dělitelné 1111.“
je dělitelné 1111.“
Ale jinak se v tom zadání asi musíš zorientovat sám.
Offline
#9 15. 11. 2010 00:50
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika zadani č.1
↑ mysteriouss: Máš dokázat, že dvě různá čísla (králíci) 201020102010... dávají stejný zbytek (králíkárna) po dělení 1111. Kolik je králíků? Kolik je králíkáren? Kolik je králíků v nejplnější králíkárně?
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#10 15. 11. 2010 01:00
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
takže mám vlastně dokázat tohle? -->
Xi bude např. 2010
Xj bude např. 20102010
a já mám zjistit jestli rozdíl těch dvou bude dělitelný 1111 tj . Xj - Xi = 20102010 - 2010 = 20100000 což tu v tom případě není, ale jestli jsem dobře pochopil co se mi celou dobu snažíš vysvětlit, tak mám dokázat, že existuje nějaké Xj - Xi které dělitelné 1111 je? Pokud ano tak mi nějak uchází ze zadání slovo "vždy" jelikož třeba tady pro ty 2 uvedené co jsem psal to neplatí.
Offline
#11 15. 11. 2010 01:09
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kombinatorika zadani č.1
↑ mysteriouss:
Řekl bych, že už to chápeš správně.
To slovo vždy patří ke slovu existují. Klidně si ho nahraď slovem „určitě“ nebo ho vynech, bude to mít stejný význam.
Offline
#12 15. 11. 2010 01:13
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika zadani č.1
↑ mysteriouss: S takovouto interpretací návodu (bez slova "vždy") to lze vyřešit. Navíc úlohu lze řešit konstruktivně (bez Dirichleta) a pak se druhou polovinou návodu nemusíš zabývat vůbec.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#13 15. 11. 2010 01:17
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
↑ Kondr:
No kdyby bylo zadání s králíky tak možná bych do toho nebyl tak zamotaný :)
podle toho co ty jsi teď napsal, tak z toho chápu, že mám zjišťovat jestli budu mít vždy stejný zbytek po vydělení rozdílu těch dvou čísel. Tam se o zbytku ale nic nepíše :(
↑ BrozekP:
Děkuji za trpělivost se mnou snad jsem už pochopil co se po mě chce teď ještě nějak vykoumat jak to dokázat to bude horší, ale na to bohužel už musím přít sám takže to vydím špatně. :(
Offline
#14 15. 11. 2010 03:04 — Editoval Kondr (15. 11. 2010 07:40)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Kombinatorika zadani č.1
↑ mysteriouss: Rozmysli si, že "1111 dělí x-y" a "x a y dávají stejný zbytek mod 1111" jsou dvě formulace téhož.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#16 17. 11. 2010 21:26
Re: Kombinatorika zadani č.1
↑ LadineQ: Přijde na to, jak se vyrovnat s faktem, že ne každé číslo uvedeného tvaru je dělitelné 1111.
Užití Dirichletova principu je o tolik jednodušší...
Offline
#17 18. 11. 2010 14:26
Re: Kombinatorika zadani č.1
↑ petrkovar:
To máte pravdu, jen jsem uvažoval ještě nad jiným řešením. Dirichlet je v tomto případě na místě (toho jsem už taky zvládl), jen jsem se chtěl popasovat ještě s jiným řešením, nacež mě napadla mat. indukce (nějaké konstruktivní řešení). Ale jelikož né každé číslo bude dělitelné číslem 1111, tak by to mohl být celkem problém..
Offline
#18 18. 11. 2010 14:44
Re: Kombinatorika zadani č.1
↑ LadineQ:Otázkou je, k čemu důkaz indukcí bude. Máme ukázat, že existuje řešení. Bez jednoho konkrétního příkladu (=vyřešení úlohy) nedokážeme základ indukce. Nebo bylo použití indukce míněno jinak?
Offline
#19 18. 11. 2010 15:53
Re: Kombinatorika zadani č.1
↑ petrkovar:
Je to tak no, nedošlo mi, že takový příklad by bylo velmi obtížné řešit konkrétně. Dirichletovým principem si potvrdíme, že taková čísla existují, matematická indukce by potřebovala konkrétní čísla. Zmátl mě komentář od uživatele Kondr, který napsal, že úlohu lze řešit konstruktivně (bez užití Dir. principu).
Offline
#21 30. 11. 2010 19:01
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
Tak jsem si to tady se vsim co se tu psalo procetl jeste jednou a vsiml jsem si ze nemam defakto hledat jedno to cislo ale dva se stejnym zbytkem ktere kdyz odectu tak mam vysledek ... a napadlo me .. neslo by to resit nesoudelnosti cisel?
Offline
#23 30. 11. 2010 22:39
Re: Kombinatorika zadani č.1
↑ petrkovar: princip zasuvek pro deleni rika obecne, ze pro n po sobe jdoucich prirozenych cisel je n zbytku pri deleni cislem n a to od 0 (zadny zbytek) az po (n-1); takze mam-li najit cislo beze zbytku delitelne n musim vzit alespon n prirozenych cisel; druha moznost je taky zajimava nebot nebaziruje na po sobe jdoucich cislech; pokud je a/n=x a zbytek po deleni z (tedy x*n +z=a) a zbytek po deleni b/n=y taky z, pak a-b (pro a>b) je beze zbytku delitelne n; v zadani je ale jeden problem; hledame cislo 201020102010....2010 delitelne beze zbytku, zatimco pokud najdu dve cisla tohoto typu se stejnym zbytkem a odectu je, tak je vysledek 201020102010...201000000...000 a to uz nevyhovuje zadani; ale i s tim si uz stari matematici poradili :-); jen mi prijde, ze napovedy v zadanich jsou nekdy malinko zavadejici a nejsem si tak uplne jist, jestli ucebni materialy jsou dostacujici na vyreseni (byt by dle pedagogickych zasad byt mely, alespon pro zakladni reseni) :-); i tak je matematika nadherna;
Offline
#24 30. 11. 2010 22:55
Re: Kombinatorika zadani č.1
Já myslím, že nápověda dláždí cesu i k správnému vyřešení problému, že sice číslo 201020102010...201000000...000 nevyhovuje zadani, ale (zapsáno ve správném tvaru) nám něco poví i jakémsi čísle vyhovujícímu zadání.
Offline
#25 09. 12. 2010 00:22
- mysteriouss

- Příspěvky: 47
- Reputace: -1
Re: Kombinatorika zadani č.1
chtěl bych se zeptat zda budou někde k vidění výsledky projektů jak to mělo vypadat aby za každý příklad bylo uděleno 5bodů popřípadě za každý těch maximum 10bodů
Offline
Stránky: 1 2
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Kombinatorika zadani č.1 (TOTO TÉMA JE VYŘEŠENÉ)
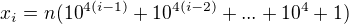 je dělitelný číslem 1111?
je dělitelný číslem 1111?