Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 11. 2010 15:13
kombinatorika projekt3
Mám zadán projekt č3.
Kombinatorika
Na šachovnici postavíme dvě dámy na dvě různá náhodně vybraná pole.
a) Jaká je pravděpodobnost, že se dámy budou ohrožovat?
b) Úlohy zobecníme na šachovnici n × n polí pro n sudé. Jaká je pravděpodobnost, že se dvě dámy budou ohrožovat?
c) Úlohy zobecníme na šachovnici n × n polí pro obecné n. Jaká je pravděpodobnost, že se dvě dámy budou ohrožovat?
A) by to mela byt pouze kombinace C(32,2)+C(32,2) add 2x protoze jednou musi byt obe damy na bilem a podruhe na cernem poli?
B) to same co u A) az nato ze budu scitat pouze pole 2x2,2x4,2x6,2x8,4x2,4x4,4x6,4x8 atd. takze budu scitat C(2,2)+C(2,4)+C......?
C) a tady si nejsem vubec jisty jak to pocitat...
Offline
#2 16. 11. 2010 15:42
Re: kombinatorika projekt3
↑ zlamal89:Ne, dámy mohou být na libovolném poli (barvu ctí jen střelci).
Offline
#3 18. 11. 2010 00:59 — Editoval kotipelto (18. 11. 2010 01:16)
- kotipelto

- Místo: Klimkovice
- Příspěvky: 40
- Škola: VŠB
- Pozice: Z půli student z půli těžce pracující
- Reputace: 0
Re: kombinatorika projekt3
Co třeba takhle:
a)
Při bližším zkoumání jsem zjistil, že na šachovnici 8x8 exituje:
28 polí takových, kdy dáma pokrývá 21 polí
20 takových, kdy dáma pokrývá 23 polí
12 takových, kdy dáma pokrývá 25 polí
a 4 pole taková, kdy dáma pokrývá 27 polí
Při výpočtu průměrné hodnoty "pokrytí dámy" E(A)
Nejdříve vložíme první dámu do pole s průměrným pokrytím E(A) polí na libovolné pole s pravděpodobností 1/64.
Po té druhou dámu s pravděpodobností 1/63. A pravděpodobnost, že první dáma ohrožuje druhou, by měla být právě
ta, kdy vkládám druhou dámu do nebezpečné zóny E(A) polí. Čili 1/63 * E(A) = E(A)/63.
b,c)
Jen zobecnit pozorování z příkladu a.
Offline
#7 23. 11. 2010 18:35
Re: kombinatorika projekt3
Zdravím
já došel se svým výpočtem k výsledku pro šachovnici 8x8 -> 0.3611 což by žřejmě asi mělo odpovídat, když šachovnice 2x2 má pravděpodobnost 1.
Výpočet je ve tvaru zlomku s jednou sumou a chtěl jsem se zeptat v jakém tvaru by to mělo být
Offline
#10 24. 11. 2010 12:21
Re: kombinatorika projekt3
↑ kotipelto:Suma zjednodušit jde. Jen se musí využít zámé vztahy (dělali jsme na cvičení) pro 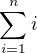 a
a 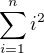 .
.
Offline
#11 25. 11. 2010 00:07 — Editoval kotipelto (25. 11. 2010 00:52)
- kotipelto

- Místo: Klimkovice
- Příspěvky: 40
- Škola: VŠB
- Pozice: Z půli student z půli těžce pracující
- Reputace: 0
Re: kombinatorika projekt3
Jo, neuvědomil jsem si, že suma polynomu lze rozdělit na sumu každého členu zvlášť... Ještě jsem se chtěl zeptat, zda pro úplné zobecnění (pro obecné n) stačí přidat k n/2 horní celou část tohoto výrazu, protože pro liché číslo by n/2 bylo necelé číslo. V pozorování, kdy jsem si to zkoušel zobrazit pro různé liché n to tak vycházelo.. Stačí dokázat toto tvrzení slovně, nebo matematickým důkazem ?
Offline
#12 25. 11. 2010 07:40
Re: kombinatorika projekt3
↑ kotipelto:Nerozumím otázce.
Důkaz je něco jiného než "silné přesvědčení" a "zbožné přání" ale také inež "platné ale nedokázané tvrzení".
Offline
#14 26. 11. 2010 20:15
Re: kombinatorika projekt3
děkuji za částečné vysvětlení uvedeného problému Kotipeltovi a Ferradovi. Vážím si toho, že se snažili vysvětlit nebo nakopnout správným směrem. Bohužel na kombinovaném studiu s dvěmi dětmi není toho času tolik a ještě, když zaměstnavatel požaduje vysokou školu, i když je nepoužitelná v praxi v mém oboru, tak to k motivaci nepřidá. Každopádně děkuju a budu doufat, že na správný postup včas přijdu.
Martin
Offline
#15 26. 11. 2010 20:53
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: kombinatorika projekt3
↑ shit: Nehledal bych vzorce, spíš se pokusil použít osvědčené "rozděl a panuj" -- rozdělit stavy, kdy se dámy ohrožují na ty, kdy
1) stojí ve stejném řádku
2) ve stejném sloupci
3) na stejné úhlopříčce.
Úlohy 1) a ž 3) jsou snadnější než původní (ve 3) se využijí výše zmíněné sumy).
Jen mimochodem ... jaký je to obor, ve kterém je daná VŠ nepoužitelná?
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#20 02. 12. 2010 11:52 — Editoval kotipelto (02. 12. 2010 11:56)
- kotipelto

- Místo: Klimkovice
- Příspěvky: 40
- Škola: VŠB
- Pozice: Z půli student z půli těžce pracující
- Reputace: 0
Re: kombinatorika projekt3
Dobrý den,
Narazil jsem na problém, který jsem si uvědomil, a to že při poli NxN, kdy n je liché. Mě v mém vztahu vždy nadbývá jedno (prostřední) pole. Vymyslel jsem způsob jak to vyřešit vzorec + 1 * ( n mod 2) * počet polí, které ohrožuje dáma (odvozeno vzorcem).Tzn. při lichém (n mod 2 = 1) se přičte a při sudém ne. Nevím však, zda toto řešení je vhodné (myslím to modulo). :-)
Offline
#21 02. 12. 2010 16:43
Re: kombinatorika projekt3
↑ kotipelto:Asi ano, ale možná se zbytečně trápíte.
Stačí mi jeden vzorec pro n liché a druhý pro n sudé. Sice existuje vzorec pro obě varianty společný, ale smyslem příkladu je správně pojmout kombinatorickou úvahu, což dva vzorce splní dostatečně.
Offline
#22 04. 12. 2010 12:56
- kotipelto

- Místo: Klimkovice
- Příspěvky: 40
- Škola: VŠB
- Pozice: Z půli student z půli těžce pracující
- Reputace: 0
Re: kombinatorika projekt3
↑ polepe: vypočti si střední hodnotu, hodnoty máš v 3tím přizpěvku. Je to pouhé dosazení do vzorce. Potom pravděpodobnost je E(A) / 63. Víc už poradit nemůžu.
Offline