Matematické Fórum

Alesak · 20. 04. 2008 19:44

ahoj,
mam problem dokazat ze 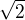$\sqrt2$ je iracionalni cislo.

vim ze se ma postupovat sporem, to znamena ze predpokladame ze to je racionalni cislo, a de vyjadrit ve tvaru $\sqrt{2} = \frac{p}{q}$ . to umocnime a dostaneme $2 = \frac{p^2}{q^2}$ , $2q^2 = p^2$ . a ted je v polakovi napsano ze sme dosli ke sporu, ale nejak tam nemuzu nic najit. poradil by nekdo co s tim?

jeste neco. jestli to dobre chapu, dukaz sporem znamena, ze musime dokazat ze neplati negace z toho vyroku, co chceme dokazat. a negace sou vsechny moznosti, kdy neplati ten vyrok, a my musime vsechny ty moznosti vyvratit. ted me zadnej nazornej priklad nenapada, ale je to spravne?

Paulus · 20. 04. 2008 20:04

Nějak jsi zapomněl na předpoklad, že p a q jsou nesoudělná čísla. Ze zápisu 2q² = p² je zřejmé, že jsou soudělná, což je spor s předpokladem nesoudělnosti.

Důkaz sporem funguje tak, jak píšeš. Je potřeba dokázat, že z negace nějakého výroku plyne spor (nepravda).

Matematické Fórum

#1 20. 04. 2008 19:44

Důkaz sporem

#2 20. 04. 2008 20:04

Re: Důkaz sporem

Zápatí