Matematické Fórum

halogan

Dobrý den,

mám následující úlohu za úkol

a nějak z toho nejsem chytrý. Přiznám se, že Poissonovo rozdělení nemám úplně pod palcem.

Měli jsme nějakou větu, která je opačnou implikací. Že pokud jsou dvě nezávislé náhodné proměnné vlnka POI, tak i jejich součet je vlnka POI. Teď jak ukázat opak.

Ocením nějaký výkop, abych mohl něco dostudovat a pokusit se to ukázat.

Děkuji.

Edit: zkusil jsem si hrát s $E(V_1V_2)$ , zda z toho dostanu $E(V_1)E(V_2)$ , tak uvidíme, zda to je správná cesta. Došel jsem k tomu, že by se muselo rovnat $p\mathrm{Var} (X) = p^2 \mathrm{Var} (X)$ .

Pavel Brožek · 21. 11. 2010 14:37

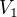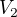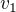Počet vylíhnutých vajec $V_1$ má nějaké rozdělení a stejně tak počet nevylíhnutých vajec $V_2$ má nějaké své rozdělení. Také počet vylíhnutých a nevylíhnutých mají dohromady nějaké rozdělení $V\equiv(V_1,V_2)$ . Označme pravděpodobnost, že se vylíhne $n$ vajec $P_1(n)$ a pravděpodobnost, že se nevylíhne $n$ vajec $P_2(n)$ . Pravděpodobnost, že se vylíhne $v_1$ vajec a zároveň nevylíhne 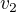$v_2$ vajec, označme $P(v_1,v_2)$ . Máš ukázat, že $P(v_1,v_2)=P_1(v_1)P_2(v_2)$ . Mám pravdu? (Jen se ujišťuji, že tomu správně rozumím, to zatím nemá být pomoc, ta snad přijde, až mi to potvrdíš :-) ).

halogan · 21. 11. 2010 14:44

↑ BrozekP:

Vypadá to tak.

Stýv · 21. 11. 2010 14:49

↑ BrozekP: takhle jsem to pochopil taky, a dá se to upočítat. žádná šikovná věta, která by ušetřila práci, mě nenapadá

Pavel Brožek

↑ halogan:

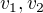Tak bych našel pravděpodobnosti $P_1(n)$ , $P_2(n)$ a $P(v_1,v_2)$ a dokázal, že rovnost $P(v_1,v_2)=P_1(v_1)P_2(v_2)$ skutečně pro každé $v_1, v_2$ platí.

Edit: Tady ani není nutné o Poissonově rozdělení vědět něco jiného než jeho tvar, který se při výpočtu použije.

Edit2: A ještě poznámka – nedokazuješ opak toho, že součtem dvou veličin s Poissonovým rozdělením je nová veličina opět s Poissonovým rozdělením, tedy že pokud součet dvou veličin má Poissonovo rozdělení, pak i jednotlivé veličiny mají Poissonovo rozdělení. Tady využíváme toho, že při daném počtu vajec je rozdělení počtu vylíhnutých vajec dáno binomickým rozdělením (to plyne z textu).

halogan · 21. 11. 2010 17:44

Mohl bych poprosit ještě o nějaké popostrčení? I přesto, že se statistice věnuji takřka denně, nejsem schopen něco lidské vymyslet. V tomto případě ani ty pravděpodobnosti. Poisson mi oproti binomickému nebo geometrickému rozdělení moc nevoní.

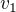Mám li dostat z $n$ vajec $v_1$ vylíhnutých, mám pravděpodobnost $P_1(v_1) = {n \choose v_1} p^{v_1} (1-p)^{n-v_1}$ , $P_2(v_2) = {n \choose v_2} (1-p)^{v_2} p^{n-v_2}$ . Což se ale po úpravě dostane na stejný výraz (krom kvantifikátoru).

A P(v_1, v_2) bude asi $P(v_1, v_2) = {n \choose v_1,v_2} p^{v_1} (1-p)^{v_2}$ .

Ale teď už si jaksi nejsem jist ničím.

Pavel Brožek · 21. 11. 2010 18:09

↑ halogan:

To ne, já ty pravděpodobnosti myslel celkově, vysčítáno přes všechny možné počty vajec. Jako že chceš tu pravděpodobnost určit ještě před tím, než vůbec víš, kolik vajec bude.

halogan

↑ BrozekP:

Takže něco jako očekávaná hodnota?

Něco jako $P_1(v_1) = \sum_{i = v_1}^{\infty} \frac{\lambda^i}{i!}\textrm{e}^{-\lambda} {i \choose v_1} p^{v_1} (1-p)^{i-v_1}$ ?

Edit: doplněno.

Pavel Brožek

↑ halogan:

Teď nevím, jestli jsi jenom zapomněl, nebo je potřeba rozebrat, proč každý člen řady musí být ještě přenásoben $\frac{\lambda^i}{i!}\textrm{e}^{-\lambda}$ . (Ta suma vlastně odpovídá rozkladu pravděpodobnosti přes úplný systém jevů, kde každý z jevů odpovídá konkrétnímu počtu všech vajec).

halogan · 21. 11. 2010 19:02

↑ BrozekP:

Není třeba, šlo jen o princip, zapomněl jsem tam dát ten počet vajec. P_2 bude tedy obdobně.

Zkusím ještě tedy P(v_1, v_2)... napadá mě ale, že tady o žádnou sumu nepůjde, protože to bude fungovat jen pro i = v_1 + v_2, takže teoreticky

$P(v_1,v_2) = {v_1+v_2 \choose v_1, v_2} \frac{\lambda^{v_1+v_2}}{(v_1+v_2)!} e^{-\lambda} p^{v_1}(1-p)^{v_2}$ — může být, nebo něco opět přehlížím?

---

Ještě mě trochu trápí různý začátek sumy u P_1 a P_2, protože je budu násobit.

Pavel Brožek

↑ halogan:

Opět ti tam chybí 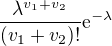$\frac{\lambda^{v_1+v_2}}{(v_1+v_2)!}\textrm{e}^{-\lambda}$

Doporučuji sumy nejprve sečíst, jde to poměrně dobře :-).

Edit: Zmiňuješ, že Poissonovo rozdělení moc nemusíš… Ale zde opravdu stačí znát jen to, že pravděpodobnost $i$ vajec (vylíhnutých i nevylíhnutých dohromady) je rovna $\frac{\lambda^i}{i!}\textrm{e}^{-\lambda}$ (kde $\lambda$ je parametr Poissonova rozdělení). Kdyby to bylo jiné rozdělení, tak bychom akorát použili jiný vzorec. Tím jsme informaci o Poissonově rozdělení použili a dál už nikde není potřeba, dál už je to jen počítání. (Samozřejmě s jiným rozdělením by se nám asi nezávislost dokázat nepodařila :-)).

halogan · 21. 11. 2010 19:08

↑ BrozekP:

Já to tam měl... jen jsem to z nejistoty smazal. Říkal jsem si, že tentokrát řeším jen pravděpodobnost, ne množství. Jdu sčítat a dám vědět.

halogan

Tak "poměrně dobře" nejde u mě aplikovat, protože řady jsem nikdy nesčítal. Pro potřeby kursu jsme si řekli, jak vyjde suma lambda^k/k! pro k od 0.

Když jsem si vyházel všechny konstanty před sumu, tak mi zbylo $\sum_{i =v_1} \frac{\lambda^i}{(i-v_1)!} (1-p)^i$

Teď kdybych si to rozšířil $\lambda^{v_1}$ a rovnou ten člen z čitatele vytknul před sumu, tak dostanu

$\sum_{i =v_1} \frac{\lambda^{i-v_1}}{(i-v_1)!} (1-p)^i$

Kde první část jde na e^\lambda, druhá je geometrická řada. Takto v součinu ale nevím, co s tím :(

Pavel Brožek · 21. 11. 2010 19:32

↑ halogan:

Ještě si před sumu vytáhni $(1-p)^{v_1}$ , pak už snad uvidíš (případně si pak vypiš pár prvních členů, to už určitě uvidíš).

halogan · 21. 11. 2010 19:38

Chápu, že si obě sumy mohu upravit na $K \sum_{k=0}^{\infty} \frac{\lambda^k}{k!} (1-p)^k$ , ale co s tím?

Omlouvám se za neznalost, ale tady opravdu nevím.

Pavel Brožek · 21. 11. 2010 19:40

↑ halogan:

To se neomlouvej :-). Já se jen snažím napovídat minimum, aby sis na to mohl přijít sám.

Zkus použít $a^x\cdot b^x=(ab)^x$ .

halogan · 21. 11. 2010 19:46

↑ BrozekP:

To je hezké :-)

Takže $\textrm{e}^{\lambda - \lambda p}$ ? Přihodím k tomu ty konstanty a uvidíme, zda se to bude rovnat.

Ale napřed se dodívám na Big Bang Theory.

---

Děkuji moc pěkně za postupné rady, ještě se ozvu.

Pavel Brožek · 21. 11. 2010 19:47

↑ halogan:

jj, to je dobře :-)

halogan · 21. 11. 2010 20:10

Dobré, vyšlo to, rovná se to.

Děkuji, přeji příjemný zbytek večera, já to jdu vyTeXovat.

Pavel Brožek · 21. 11. 2010 20:14

↑ halogan:

Tobě taky.

Matematické Fórum

#1 21. 11. 2010 14:04 — Editoval halogan (21. 11. 2010 14:09)

Nezávislost u Poissonovy distribuce

#2 21. 11. 2010 14:37

Re: Nezávislost u Poissonovy distribuce

#3 21. 11. 2010 14:44

Re: Nezávislost u Poissonovy distribuce

#4 21. 11. 2010 14:49

Re: Nezávislost u Poissonovy distribuce

#5 21. 11. 2010 14:49 — Editoval BrozekP (21. 11. 2010 15:16)

Re: Nezávislost u Poissonovy distribuce

#6 21. 11. 2010 17:44

Re: Nezávislost u Poissonovy distribuce

#7 21. 11. 2010 18:09

Re: Nezávislost u Poissonovy distribuce

#8 21. 11. 2010 18:25 — Editoval halogan (21. 11. 2010 19:03)

Re: Nezávislost u Poissonovy distribuce

#9 21. 11. 2010 18:53 — Editoval BrozekP (21. 11. 2010 19:01)

Re: Nezávislost u Poissonovy distribuce

#10 21. 11. 2010 19:02

Re: Nezávislost u Poissonovy distribuce

#11 21. 11. 2010 19:07 — Editoval BrozekP (21. 11. 2010 19:08)

Re: Nezávislost u Poissonovy distribuce

#12 21. 11. 2010 19:08

Re: Nezávislost u Poissonovy distribuce

#13 21. 11. 2010 19:24 — Editoval halogan (21. 11. 2010 19:32)

Re: Nezávislost u Poissonovy distribuce

#14 21. 11. 2010 19:32

Re: Nezávislost u Poissonovy distribuce

#15 21. 11. 2010 19:38

Re: Nezávislost u Poissonovy distribuce

#16 21. 11. 2010 19:40

Re: Nezávislost u Poissonovy distribuce

#17 21. 11. 2010 19:46

Re: Nezávislost u Poissonovy distribuce

#18 21. 11. 2010 19:47

Re: Nezávislost u Poissonovy distribuce

#19 21. 11. 2010 20:10

Re: Nezávislost u Poissonovy distribuce

#20 21. 11. 2010 20:14

Re: Nezávislost u Poissonovy distribuce

Zápatí