Matematické Fórum

Saturday · 21. 04. 2008 22:11

Ve skriptech: http://kam.mff.cuni.cz/~pultr/ma.pdf na straně 121 (stránkování PDF dokumentu) je dole pozorování, které říká, že dolní R. integrál Dirichletovy funkce je roven 0 a horní je roven 1.

Jak je to možné?

Moje představa byla taková, že Dirichletova funkce je nespojitá v každém bodě a že dolní (resp. horní) integrál je definován pomocí sumy obsahů malých obdélníčků (tedy mám nějaké rozdělení D). Nicméně u nespojité funkce žádné rozdělení přece nemá smysl zavést nebo ano?

Díky za pomoc

robert.marik · 21. 04. 2008 22:31

obdélníčky "aproximují funkci zdola a shora"
u dirichletovy funkce je na každém intervalu minimum (a infimum) nula a maximum (a supremum) jedna. V dolnim integralu jsou tedy obdelnicky s nulovou vyskou, v hornim integralu s vyskou jedna. Se spojitosti to nijak nesouvisi, jenom s ohranicenosti.

Saturday · 21. 04. 2008 22:43

> u dirichletovy funkce je na každém intervalu minimum (a infimum) nula a maximum (a supremum) jedna. V dolnim integralu jsou tedy obdelnicky s nulovou vyskou, v hornim integralu s vyskou jedna.
s tim souhlasim

Ale podle té definice musí mít ty obdélníčky nějakou šířku, ne? Vždy? integrál, a? už horní nebo dolní vyjadřuje nějakou plochu (alespon podle definice v odkazovanych skriptech)

Myslel jsem, že ta nespojitost tam hraje tu roli, že ani nemůžu ty obdélníčky zúžovat.

robert.marik · 21. 04. 2008 23:18

Pokud integruji na [0,1] tak libovolne rozsekani tohoto intervalu na podintervaly je deleni. A v rimannove integralu se obvykle uvazuji vsechna mozna deleni (supremum nebo infimum pres vsechna deleni). -- jde to jeste i delat pres nulovou posloupnost deleni (posloupnost deleni takova, ze norma tech deleni jde k nule). Ale to deleni nema s funkci co delat.

Rodelim na 100 stejnych dilku, potom na 1000000 dilku, potom na 100000000 dilku a obrazek k dolnim a hornim souctum bude vypadat porad stejne, jenom obdelnicky budou mit zakladnu nejprve 1/100, potom 1/1000000 atd.

Saturday · 21. 04. 2008 23:26

uz chapu, diky

Marian · 22. 04. 2008 15:50 — Editoval Marian (22. 04. 2008 17:39)

Jen bych mirne doplnil, ze existuji i jine definice integralu (napr. Lebesgueova definice), kde je dokonce mozno spocitat (Lebesgueuv) integral Dirichletovy funkce na intervalu [0,1]. Ukazuje se, ze pomoci Lebesgueovy definice je tento integral roven nule. Konstrukce Lebesgueova integralu ale vyzaduje nektere hlubsi poznatky o topologii realne primky a take pojem meritelnosti.

andrew · 22. 04. 2008 16:32

2Marian : Zdravim, to co jste uvedl je pravdive az na vetu

Ukazuje se, ze pomoci Lebesgueovy definice je tento integral roven jednicce.

Bohuzel zde pravdu nemate. Integral z Dirichletovy funkce je roven nule.

Marian · 22. 04. 2008 17:38

↑ andrew:

Samozrejme, ze je to nula. Clovek na to mysli a pak na to take zapomene. Dekuju. Samozrejme je pravda, ze ten integral se rovna nule.

Saturday · 22. 04. 2008 18:38

@Marian: Na Lebesguuv integral jsem se taky ze zajimavosti podival, ale odradila me Lebesguova mira..

Kdyz uz je rec o integralech, jaky je hlavni rozdil mezi Newtonovym a Riemannovym integralem? Popřípadě, pokud o tom máte někdo nějaký pěkný material, tak bych rozhodně nepohrdnul ;-)

robert.marik · 22. 04. 2008 22:02

Nektere funkce jsou integrovatelne podle Riemanna a podle Newtona ne. napriklad .... ted me nic nenapada, asi cokoliv co ma bod nespojitosti, nevim presne co se mysli tim Newtonovym inetgralem, je myslim vic definic.

Nektere naopak, treba 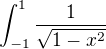$\int_{-1}^1\frac1{\sqrt{1-x^2}}$ je integrovatelna podle newtona (je to nějaký arkusisinus) a není podle Riemanna (neohraničená funkce)

Pokud oba integraly existuji, tak jsou stejne.

Divil bych se , kdyby to nebylo pekne vysvetlene v Jarnikovi. Ale nemam ho poruce.

Saturday · 26. 04. 2008 14:37

↑ robert.marik: Diky za pomoc

P.S.: Nasel jsem to v Jarnikovi I1 - str. 165, jsou tam i hezke priklady ;-)

Matematické Fórum

#1 21. 04. 2008 22:11

Dolní a horní Riemannův integrál Dirichletovy funkce

#2 21. 04. 2008 22:31

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#3 21. 04. 2008 22:43

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#4 21. 04. 2008 23:18

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#5 21. 04. 2008 23:26

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#6 22. 04. 2008 15:50 — Editoval Marian (22. 04. 2008 17:39)

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#7 22. 04. 2008 16:32

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#8 22. 04. 2008 17:38

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#9 22. 04. 2008 18:38

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#10 22. 04. 2008 22:02

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

#11 26. 04. 2008 14:37

Re: Dolní a horní Riemannův integrál Dirichletovy funkce

Zápatí