Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 11. 2010 22:25
Aritmetika
Ahoj mám tu jeden takýto príklad a moc si neviem s ním rady...
Určite všetky dvojice prirodzených čísel x, y, pre ktoré platí:
Nejaké nápady ? :)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
- (téma jako vyřešené označil(a) hradecek)
#2 25. 11. 2010 11:46
Re: Aritmetika
↑ hradecek:![kopírovat do textarea $8x^3-y^2=387 \nl 8x^3=387+y^2 \nl x^3=\frac{y^2+387}{8} \nl x=\sqrt[3]{\frac{y^2+387}{8}} \nl x=\frac{1}{2}\sqrt[3]{y^2+387}$](/mathtex/34/341b944b769d96a260c0983df2cc662d.gif)
teď musíš zkoumat podmínky odmocnitelnosti 3 a dělitelnost 2
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#3 25. 11. 2010 14:06
Re: Aritmetika
↑ hradecek:

 to ale znamená, že
to ale znamená, že 
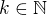

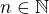
jenomže poslední rovnice nikdy neplatí, protože  musí být liché číslo a druhá mocnina lichého čísla dává po dělení osmi zbytek 1.
musí být liché číslo a druhá mocnina lichého čísla dává po dělení osmi zbytek 1.
Rovnice nemá v přirozených číslech řešení.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 25. 11. 2010 14:23
#5 25. 11. 2010 18:00
Re: Aritmetika
↑ zdenek1:
Nj super, dík.
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline

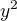 třeba
třeba 