Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 22. 04. 2008 19:45
Re: Slovné Matematické Úlohy
↑ breaker:Zkusím ten první příklad : Uvažuji takto :
21g ......7 dílků čokolády
x g ......9 dílků čokolády ....
---------------------------------- ..
.. 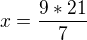 ..
.. 
Celá čokoláda má hmotnost 21+27=48g. Vyšrafovaný kousek je 1/16 ze 48g .. což odpovídá 3g .
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#3 22. 04. 2008 19:59 — Editoval Paulus (25. 04. 2008 17:13)
Re: Slovné Matematické Úlohy
↑ Ivana:
Myslím, že nemáte pravdu. Ta trojčlenka bude fungovat jen v případě, že všechny dílky váží stejně. To ale neváží.
Já bych postupoval takto: označím si jednotlivé dílečky písmeny:
A | B | C | D
E | F | G | H
I | J | K | L
M| N | O | P
Protože obdélník F je při stejné "výšce" třikrát těžší než obdélník E, musí být i B třikrát těžší než A.
B tedy váží 3.2g=6g.
Protože obdélník K je při stejné "výšce" dvakrát těžší než obdélník J, musí být i C dvakrát těžší než B.
C tedy váží 2.6g=12g.
Protože obdélník P je při stejné "výšce" dvakrát těžší než obdélník O, musí být i D dvakrát těžší než C.
Hledaná hmotnost D je tedy 2.12g=24g.
Offline
#4 22. 04. 2008 20:03 — Editoval Fabo (22. 04. 2008 20:04)
Re: Slovné Matematické Úlohy
Druhý = výsledok je 3 na 21 čiže nejakých 10 460 353 203 korún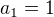
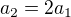
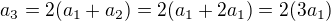
Tu si môžeš všimnú? jednu vec, ktorú tu rovno použijem, a to: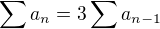
čo sa dá rekurzívne vyjadri? až k: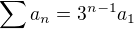
7902 5 01 gymnázium - matematika - Okt.... holt maturity
-------------------------------------------------------------------
Bejvávalo. Momentálne FMV B-ME-MO prez [sem. 5, E] a s tym spojena matematika a statistika ma sem opat priviala.
Offline
#7 22. 04. 2008 20:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovné Matematické Úlohy
↑ Ivana:↑ Paulus:
Zdravim vas, ja bych to delala takto: oznacim postupne pomoci pismen strany obdelnicku, pokud je to stejna strana, tak je to stejne pismeno:
2=ab
1=ac
3=cd..... a tak to cele obejdu, az dojdu k obsahu hledaneho obdelnicku.
Ted zacnu postupne vyjadrovat z 1. rovnice a a dosadim do druhe, pak c a dosadim do 3 a tak pokracuji az do konce. Nejak to neupravuji, ani nekratim - trva to chvilku.
Vysledek mam take 24.
Offline
#8 23. 04. 2008 23:10
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Slovné Matematické Úlohy
↑ breaker: Mohu se zeptat na zdroj těch úloh?
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#10 24. 04. 2008 17:44
Re: Slovné Matematické Úlohy
↑ breaker:
Me se moc libi ten posledni kresleny hlavolam...bohuzel na tom obrazku casto nerozpoznam, co je tam nakresleno :-( A kdyz jo, neviem, ako sa to poveda po slovensky:-D
Offline
#11 24. 04. 2008 23:15
Re: Slovné Matematické Úlohy
Spocitala jsem tu 4 (Dostihy)...za spravnost nerucim a za to, ze muj postup pochopite taky ne ;-)
Nejprve jsem to pocitala uplne obecne, ale to byste me asi ukamenovali, takze to tu prevedu na vypocet s konretnimi cisly.
1. Urcim, jak dlouha je trat, na ktere se bezi, oznacim ji d.
Tak kun se zokejem ubehl 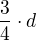 . Pak se kun bez zokeje vracel ke startu a to ubehl
. Pak se kun bez zokeje vracel ke startu a to ubehl  z techto
z techto 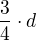 , tj.
, tj. 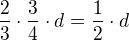 . Tim se dostal do vzdalenosti
. Tim se dostal do vzdalenosti 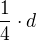 od startu. Do cile mu zbyvala vzdalenost
od startu. Do cile mu zbyvala vzdalenost 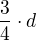 . Vse je na obrazku 1. Odtud je i videt (nebo si to muzete overit sectenim trech zlomku), ze kun timto pobihanim sem a tam ubehl puvodni delku trati dvakrat. Protoze je uvedeno, ze ubehl 2400 m, ma trat dostihu delku 1200 m .
. Vse je na obrazku 1. Odtud je i videt (nebo si to muzete overit sectenim trech zlomku), ze kun timto pobihanim sem a tam ubehl puvodni delku trati dvakrat. Protoze je uvedeno, ze ubehl 2400 m, ma trat dostihu delku 1200 m .
2. Jakou rychlosti beha kun?
Pokud mu trat 1200 m trva normalne 60 s, beha kun rychlosti: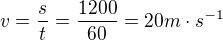
3. Ted jeste jednou, ale uz s konkretnimi cisly vzdalenosti, trat ma 1200 m, sledovat vse muzete na obrazku 2.
a) Kun se zokejem bezel 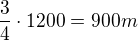 ,
,
b) Kun bez zokeje se vracel ke startu 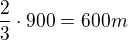 , tim se dosal do vzdalenosti 300 m od startu.
, tim se dosal do vzdalenosti 300 m od startu.
c) Kun se rozbehl zase k cili a zokej proti nemu. Jsou od sebe 600 m (viz obrazek 2). Zokej byl dvakrat pomalejsi nez kun, takze kdyz se potkali, urazil z tech 600 m kun dve tretiny vzdalenosti, tj. 400 m a zokej jednu tretinu, tj. 200 m.
d) Potkali se ve vzdalenosti 700 m od startu (500 m od cile, viz obrazek 2) a pelasili spolu do cile.
4. Zname uz odpoved na otazku kolik metru bezel zokej naproti Kenovi......200 m.
5. Spocitame jak dlouho jim trval zavod. Pouzijeme obrazek 2.
Cervene sipky oznacuji, kdy bezel kun se zokejem (rychlosti 20 m/s)......900+500=1400 m,
modre sipky odpovidaji situaci, kdy bezel kun sam (polovicni rychlost, tzn. 10 m/s)......600+400=1000 m.
Vyjdu ze vztahu pro rychlost, odkud si vyjadim cas t:
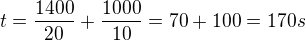
Takze odpoved na otazku, za jak dlouho probehli spolecne cilem by bylo 170 s od startu zavodu.
Offline
#13 25. 04. 2008 19:41
Re: Slovné Matematické Úlohy
Tak zkusím příklad 4 (tenisový oddíl)
Ptáme se, kolik je tenistů v oddíle - označme si tento počet n. Kolik je možností vybrat dvojici? Zřejmě 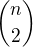 (Mimochodem, anglicky se to čte "n choose 2", což doslova znamená "vyber dva z n". Myslím, že je to důvtipnější pojmenování než české (slovenské) "n nad dvěma".)
(Mimochodem, anglicky se to čte "n choose 2", což doslova znamená "vyber dva z n". Myslím, že je to důvtipnější pojmenování než české (slovenské) "n nad dvěma".)
Kolik je způsobů na výběr trojice?  . Má platit, že trojice se dají vybrat třitkrát více způsoby než dvojice:
. Má platit, že trojice se dají vybrat třitkrát více způsoby než dvojice: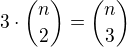


Tenisový oddíl má tedy 11 členů. (Mimochodem u 11 členů nevěřím tomu, že jsou všichni stejně dobří..)
Offline
#14 25. 04. 2008 19:53 — Editoval Jorica (25. 04. 2008 19:57)
Re: Slovné Matematické Úlohy
↑ Paulus:
Diky za pochvalu grafu...chvili jsem v tom hledala ironii, protoze pokud mate/mas na mysli ty barevne sipky, pripadne jine obrazky co sem vkladam, tak to je prosim vse vytvory ala Panel kresleni v MS WORD :-D No a ty popisky, nevim, musela bych zapnout notas...vcera vecer jsem sedela u nej a mam tam Office 2007 a tam je jako vychozi font neco neobvykleho, zadnej Arial nebo Times, tak tim je to popsane, primo v Editoru rovnic (v novych Office se to mozna jmenuje jinak, nez editor rovnic).
Jinak pekne reseni tenistu, ja na tenhle vzorecek pro kombinacni cisla zapominam a vse si hned rozepisuju....takze moje reseni, co tu mam na papire, nebylo tak elegantni ;-)
A pochybnosti o tom, ze vsech 11 clenu oddilu je stejne dobrych, jsou asi zbytecne, kdyz si prectu, co vse zvladl ten splasenej kun :-)))))))
Offline
#15 25. 04. 2008 23:30 — Editoval Jorica (26. 04. 2008 13:06)
Re: Slovné Matematické Úlohy
Tak mi ten rebus nedal a mozna jsem ho rozlouskla ;-) Jedine, co mi tam nesedi je KRB, protoze jsem zila v domneni, ze slovensky je to KOZUB ;-)
ODCITANIM je mysleno "vyruseni" stejnych pismen. (Nemusi byt primo vedle sebe, jak je to v napovede, ale musi byt ve stejnem poradi zleva doprava).
ODMOCNENI je "vyruseni" zdvojenych shluku pismen.
EXPONENT -1 prepis pismen slova pozpatku (zprava-doleva).
ABSOLUTNI HODNOTA rusi diakritiku.
Pak by to bylo takto (je to bez tech abs. hodnot, protoze diakritiku do matematicke sazby TEXu nedostanu).![kopírovat do textarea $ARCHA-\(KRAB-KRB\)+\(\sqrt{MIMINO-\[NOTA-\(VESTA-\(SEV\)^{-1}\)\]}\)^{-1}+$](/mathtex/d5/d5319d031ef7290faae11f6e94ca941c.gif)
![kopírovat do textarea $\{SEDLO-\(PASTA-PATA\)-\[MYDLO-\(DYM\)^{-1}\]\}+\(KOSE-\(KOMAR-$](/mathtex/61/61cd7c77d685c3bdc5d6c499c2547eba.gif)

Az na malou nepresnost, ze od slova ARCHA se ma odecist A a neni patrne ktere, se uz pak da dopatrat k tomu, ze tajenkou je ARCHIMEDES.
Offline
#16 27. 04. 2008 16:38
Re: Slovné Matematické Úlohy
K úloze 5 - Kdo je kdo?
Protože jde jen o tři osoby, rozeberu všechny možnosti. Těch je 3!=6, takže to snad nebude takový problém.
Uvedené čtyři podmínky jsou vlastně čtyři implikace. Připomínám, že implikace je pravdivá, pokud z pravdy plyne pravda a pokud z nepravdy plyne cokoliv. Jediná možnost, kdy je implikace nepravdivá je, když z nepravdy plyne pravda. Uvedené implikace si očísluju a pak sestavím tabulku.
1. M je U => L je Ř
2. L je Ř => l je M
3. L není U => K je Ř
4. K je M => M je Ř
Tabulka všech možností:
K | L | M || 1. | 2. | 3. | 4.
U | Ř | M || a | a | N | a
U | M | Ř || a | a | N | a
Ř | U | M || a | a | a | a - toto je řešení
Ř | M | U || N | a | a | a
M | Ř | U || a | a | N | N
M | U | Ř || a | N | a | a
Krkoš je řidič, Lepko je úředník a Mahula je manažér.
Offline
#19 23. 09. 2008 22:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Slovné Matematické Úlohy
↑ breaker:
Zdravím :-)
úlohy jsou z aktuální soutěži - dle pravidel fóra není možné řešit.
Můžeš se podívat na názorů kolegů a zvolit si další postup podle těchto názorů http://forum.matweb.cz/viewtopic.php?id=872
A? se daří :-)
-------------------------
Na jednu hádanku odpovědet smím (je mimo soutěž) - Rozdíl mezi Kofolou a matikou není žádný :-)
Offline


