Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 11. 2010 09:55
goniometricke funkcie
Dobry den,
Mam takuto ulohu:
Zistite hodnotu goniometrickych funkcii sin,cos,cotg pre  ak tg x = -5/12.
ak tg x = -5/12.
NA cotg som prisiel ze je cotg x = -12/5. lenze pre sin a cos neviem ako nato. viem ze mam pouzit vzorec tgx= sinx/cosx.
mohli by ste mi troska pomoct, nepotrebujem uplne riesenie chcem to sam vypocitat, len troska pomoct potrebujem.
Offline
- (téma jako vyřešené označil(a) faktorial)
#2 28. 11. 2010 10:14
Re: goniometricke funkcie
↑ faktorial:
Ahoj pokud nejsou žádná omezení není nic snažšího než zjistit pomocí kalkulačky úhel, pro který má tg hodnotu -5/12 následně z toho udělat sin a cos pomocí kalkulačky.
"Vím, že nic nevím." Sokrates
Offline
#4 28. 11. 2010 10:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricke funkcie
↑ faktorial:
Zdravím,
potom je třeba zvolit jiný vztah, ve kterém se vyskytuje tg(x) a pouze cos(x) nebo pouze sin(x) - viz tabulka a nezapomenout na dodržení správného kvadrantu.
Offline
#6 28. 11. 2010 11:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricke funkcie
↑ faktorial:
platí, je to stejné jako 2. mocnina zde 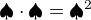
Offline

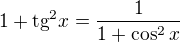
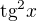 funkciu na druhu,plati toto:
funkciu na druhu,plati toto: 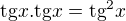 ?
?