Matematické Fórum

↑↑ Hlavson:

Z předchozích příspěvků je už snad jasné, jaká je střední hodnota počtu ok na straně kostky. Stran kostky je celkem šest. Když na jednu stranu dáš příliš mnoho ok, přidáváním ok na další strany už nemůžeš snížit střední hodnotu.

↑↑ petrkovar:

Zadání se mi zdá poněkud nejasné (plně jsem ho pochopil až z Vašich příspěvků v diskuzi).

Ze začátku zadání „Máme dvě stejné poctivé kostky. Jak rozmístit oka…“ bych si myslel, že jejich strany jsou prázdné a teprve budu oka rozmísťovat (tedy po rozmístění už nemusí být stejné).

Pokud bych uvažoval, že i po rozmístění ok mají být stejné, pak zase mám problém s pojmem „poctivé“. Kostka vyvážená tak, že strany padají s pravděpodobnostmi 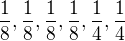, s počty ok na stranách 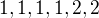je poctivá z hlediska, že každý možný výsledek má stejnou pravděpodobnost.

↑↑ petrkovar:
Mužete, prosím, upřesnit, zda kostka musí být šestistěnná ? Jinak je asi jasné podle odpovědí výše, že počet ok na jednotlivých strannách není omezen, a že se nesmí opakovat, pokud se neopakuji všechny.
Jen mi opravdu ze zadání není jasný počet stran kostky. Diky.

Chtěl bych se zeptat, zda by zadání vyhovovala tato kostka:
4,4,4,0,0,0 - respektive spadá do množiny výpočtů, ale jestli je povolená kostka která má na své straně 0 ok... možná je to blbost, ale dost to ovlivní výsledky...

↑↑ petrkovar:
Takže když se stejné počty ok mohou opakovat 2x, mohou se opakovat 3x (např. 1,1,1,5,5,5) ?
Vyhovuje zadání kostka , která má na všech stranách stejnou hodnotu (např. 2,2,2,2,2,2) ?

↑ petrkovar: Díky. Ještě to rozumně zformulovat.

↑ Voyta:Ano, kostky mají stejné hodnoty ok.