Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 11. 2010 22:18
Kombinatorika, č. 4
Jsem štastným majitelem tohoto zadání:
Máme nepoctivou kostku. Víme, že číslo 6 padá třikrát častěji než číslo 1, číslo 5 padá dvakrát častěji než číslo 2 a číslo 4 padá stejně často jako číslo 3.
a) Kolik takových kostek existuje? popište, jak vypadají všechny (nerozlišujeme umístění čísel na kostce, jen pravděpodobnosti jednotlivých stran).
b) Jaká je střední hodnota počtu ok při jednom hodu? (výsledkem není číslo, ale výraz)
c) Jaká je největší střední hodnota počtu ok při jednom hodu, které lze při vhodné konstrukci kostky dosáhnout?
b) a c) zatím neřeším, jelikož vychází z a), které mi zatím uniká. Zatím uvažuji takto - každé z čísel má základní pravděpodobnost 1/6. Ale jelikož platí, že "všechna čísla jsou si rovna, ale některá jsou si rovnější", provedu rozklad na tyto pravděpodobnosti:
P(1,2)=1/11
P(3,4,5)=2/11
P(6)=3/11
V tomto rozdělení se mi ale všechny pravděpodobnostní jevy "slijí" dohromady a chybí mi rozčlenění pro tři základní jevy (6-1, 5-2, 3-4). Kam bych měl teď vyšlápnout dál ?
Offline
#2 24. 11. 2010 22:45
Re: Kombinatorika, č. 4
Frogger napsal(a):
Zatím uvažuji takto - každé z čísel má základní pravděpodobnost 1/6.
To by platilo pro poctivou kostku. Takovou podle zadání nemáme.
Frogger napsal(a):
provedu rozklad na tyto pravděpodobnosti:
P(1,2)=1/11
P(3,4,5)=2/11
P(6)=3/11
Nerozumím Vašemu zápisu. Copak to je P(1,2)=1/11 ? Jedná se o pravděpodobnost, že padle 1 nebo 2? Pokud ano, tak součet pravděpodobností nedává jedničku.
Pokud se však jedná o (nešťastně) zkrácený zápis rovnosti P(1)=P(2)=1/11, pak jste si jen tipnul jedno možné řešení. Máte však najít *všechna* řešení. V zadání například není žádná informace, která by nás opravňovala k předpokladu, že P(5)=P(3). Platit to může, ale také nemusí.
Co zkusit dál? Zkuste formálně zapsat údaje ze zadání.
Offline
#3 25. 11. 2010 12:24
Re: Kombinatorika, č. 4
↑ petrkovar:
Dobry den,
a co kdyby sjem uvazoval takto:
P(1) = 1/12
P(2) = 1/9
P(3) = P(4) = 1/6
P(5) = 2/9
P(6) = 3/12
Dekuji za odpoved
Offline
#5 25. 11. 2010 13:03 — Editoval zdarec (26. 11. 2010 09:10)
Re: Kombinatorika, č. 4
↑ petrkovar:
Jen jsem reagoval na drivejsi prispevek, a navrhl zpusob, jakym by se zadani dalo prepsat.
Ohledne stredni hodnoty jsem se chtel zepatat na bod b) . V zadani je (výsledkem není číslo, ale výraz) , pricemz dle definice Stredni hodnoty :
Necht nahodna promenna X nabyva k moznych hodnot z mnoziny X je prvkem {h1, h2,..., hk}, kde Xi nastava s pravdepodobnosti pi a p1 + p2 + ... + pk = 1. Stredni hosnotou promenne X je pak cislo.
Chtel jsem se zeptat, zda to ma byt vseobecne zapsani dle jednotlivych kriterii, nebo je tim mysleno neco jineho.
Dekuji
...
Uz jsem to asi pochopil, mame napsat vzorec, ketry by zahrnoval vsechna mozna resesi (vyhotoveni kostky).
Offline
#8 26. 11. 2010 14:46
Re: Kombinatorika, č. 4
Podle většiny dotazů je zřejmé, že se studenti často neumí vyrovnat s faktem, že takových kostek existuje více.
Je třeba (podle zadání) správně zvolit jistou sadu parametrů, správně stanovit jejich definiční obor a správně dopočítat výsledky se zvolenými parametry.
Offline
#10 26. 11. 2010 19:16
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kombinatorika, č. 4
↑ amic:
Já bych řekl, že ano.
Offline
#11 29. 11. 2010 18:57
Re: Kombinatorika, č. 4
Zdravim, snad nebude vadit, kdyz se zde zeptam i cast projektu z teorie grafu. Chtel bych se tedy pro overeni zeptat, kolik sluzebnich cest by melo vyjit pro napriklad K9 a K10 (dost na to aby se to nekomu chtelo vypisovat rucne :)). Nejaky postup me jiz napadl a rad bych si jej pokud mozno overil. Diky
Offline
#12 29. 11. 2010 19:01
#20 29. 11. 2010 21:36
Re: Kombinatorika, č. 4
Zadne tu zatim neni, taky jsem tedka trosku zmateny. Ale mam otazku. Mam graf k3 ocislovany 1, 2 a 3 a zrusim hranu treba 1-3. Z vrcholu 2 pak nemuzu podniknout celou tu okruzni jizdu, ale pouze cestovat do vrcholu 1 a stejnou hranou zpet a pak do vrcholu 3 a stejnou hranou zpet. Bere se toto jako platna sluzebni cesta?
Offline
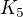 uvedené číslo není správně. Pro
uvedené číslo není správně. Pro 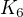 je správně.
je správně.