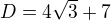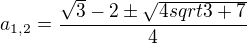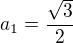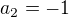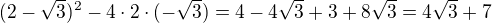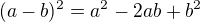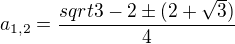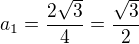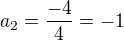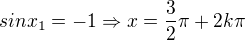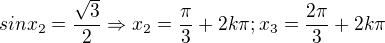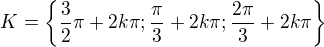Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Rovnice s parametrem + goniometrické rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 22. 04. 2008 17:16 — Editoval NIghtingale (22. 04. 2008 17:16)
- NIghtingale
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Rovnice s parametrem + goniometrické rovnice
1) a+x x-3
----- - 2 = ------
3 3
2) ax^2+2ax+4=0
3) sin^2x-cos^2x+sinx=0
4) 2sin^2x+2sinx- "druhá odmocnina ze 3" *sinx="druhá odmocnina ze 3"
S tímhle si totálně nevíme rady :D Takže prosím někoho o radu,případně nějaký návod jak na rovnice s parametrem protože ty ubec nechapu.Kdyžtak prosim postup k příkladům,moc děkuji.
Offline
#2 22. 04. 2008 17:58
Re: Rovnice s parametrem + goniometrické rovnice
1) vynasobime celou rci 3
a + x - 6 = x - 3
a = 3
zaver : a = 3 => K = R
a je z R - {3} => K = {0}
2) vypocitas diskriminant (A = a, B = 2a, C = 4)
D = 4a^2 - 16a = 4a(a-4)
ted muzes napriklad udelat tabulku kde uvidis jak bude D vypadat pro ruzne intervaly
)0( )4(
4a - + +
a-4 - - +
+ - +
zacnes hledat K pro tri mozne pripady D
D = 0 => 4a(a-4) = 0 (to jsou nulove body ktere jsme nasli)
a = 0 => po dosazeni dostanes vyraz 4 = 0 coz neplati...takze K je prazdna mnozina
a = 4 => x = -b/2a = -8/8 = 1 takze K = {1}
D < 0 => a je prvkem otevreneho intervalu (0,4) (z tabulky) ... K je prazdna mnozina
D > 0 => a je prvkem sjednoceni intervalu (-oo, 0)u(4, +oo)
-2a +- [4a(a-4)]^1/2
x1,2 = ------------------------
2a
zaver : a = 0 => K = {}
a = 4 => K = {1}
a je prvkem (0; 4) => K = {}
a je prvkem (-oo;0)u(4;+oo) => K je dvouprvkova (viz x1,2)
3) podle vzorce sin^2x + cos^2x = 1 si vyjadris cos^2x = 1 - sin^2x
dosadis : sin^2x - (1 - sin^2x) + sinx = 0 a substituujes treba : a = sinx
dosadis substituci : a^2 -1 + a^2 + a = 0
a mas kvadratickou rci : 2a^2 + a -1 = 0
ziskas koreny (treba rozklad) : (a-1)x(a+1/2)
a1 = 1 ; a2 = -1/2
a dosadis zpet do substituce :
pro a1 : sinx = 1
x = pi/2
pro a2 : sinx = -1/2
x1 = 7pi/6
x2 = 11pi/6
vysledek : K = {pi/2 + 2kpi; 7pi/6 + 2kpi; 11pi/6 + 2kpi}
Offline
#3 23. 04. 2008 14:02 — Editoval NIghtingale (23. 04. 2008 14:06)
- NIghtingale
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Re: Rovnice s parametrem + goniometrické rovnice
Jenom takovej dotaz k tý trojce,nemá tam být a1=-1 a a2=1/2 ?? Protoze kdyz vypocitam kvadratickou rci tak presne tyhle 2 koreny me vychazeji,a kdyz roznasobim to tvy (a-1)*(a+1/2) tak mi vyjde 2a^2 - a - 1 coz neni prece 2a^2+a-1 z ktere jsi rozkladal..?Mozna sem se nekde ztratil...
respektive nemělo by to tvoje rozložení vypadat (a+1)*(a-1/2) ? to už vychází :-)
Offline
#4 23. 04. 2008 16:34
Re: Rovnice s parametrem + goniometrické rovnice
↑ NIghtingale:
ano mas pravdu, koreny opravdu jsou -1 a 1/2
pro a1 : sinx = -1
x = 3pi/2 + 2kpi
pro a2 : sinx = 1/2
x1 = pi/6 + 2kpi
x2 = 5pi/6 + 2kpi
Offline
#7 23. 04. 2008 20:21
- NIghtingale
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Re: Rovnice s parametrem + goniometrické rovnice
já bych potreboval zase poradit s tímhle
u tohodle sem dosel k D=(2-3^1/2)^2-4*2*(-3^1/2)
a s touhle soustavou rovnic
3 16
------- + --------- = -1
x-1 y+3
3 88
------ + --------- = 5
x-1 y+3
----------------------------------------
díky :)
Offline
#9 23. 04. 2008 21:03
- NIghtingale
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Re: Rovnice s parametrem + goniometrické rovnice
Díky díky,to mě nenapadlo použít takhle sčítací metodu...a jeste tu goniometrickou..neví někdo?:)
Offline
#11 23. 04. 2008 21:53
- NIghtingale
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Re: Rovnice s parametrem + goniometrické rovnice
Achjo,kde všichni v tom diskriminantu berete 4*3^1/2 ?? :(
Já tam dojdu k výsledku D=(2-3^1/2)^2-4*2*(-3^1/2) =>4+3 +8*3^1/2 ne?Nebo kde mám chybu? :(
Offline
#13 23. 04. 2008 21:57
- NIghtingale
- Zelenáč
- Příspěvky: 24
- Reputace: 0
Re: Rovnice s parametrem + goniometrické rovnice
ajo ja sem blbec....dík :)
Offline
#14 23. 04. 2008 22:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s parametrem + goniometrické rovnice
↑ aritentd: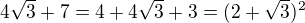 uz vidis , jak ten vysledek dostat ?
uz vidis , jak ten vysledek dostat ?
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Rovnice s parametrem + goniometrické rovnice (TOTO TÉMA JE VYŘEŠENÉ)

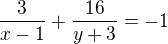
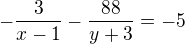
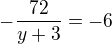
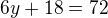
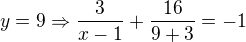
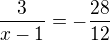
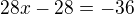
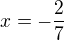
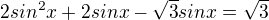
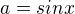 dostal k diskriminantu
dostal k diskriminantu