Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 12. 2010 23:52
Projekt 3
Dobrý den (večer),
dneska jsem slyšel o větě kolik může být v jakémkoli grafu hran pokud graf neobsahuje trojúhelníky, nemůžu si ale vspomenout jak se ta věta jmenovala a kontakt na člověka který mi o ní říkal nemám. Pomohl byste mi prosím ze zaspomínání jaký je název té věty?
děkuji Petr Sedláček
Offline
#2 02. 12. 2010 11:53
Re: Projekt 3
↑ Sedlak:
Myslim, ze taka veta nie je, ak ano tak ma opravte, velmi by to pomohlo aj mne keby taka bola :]
Asi si to pleties s dosledkom Eulerovho vzorca, tento dosledok hovori, ze v jednoduchom rovinnom grafe na v=>3 vrcholoch bez trojuholnikov je najviac 2v-4 hran. Toto plati len pre rovinne grafy, ty sa vsak pytas ci nieco take plati pre "vseobecny" graf.
Presne tuto vetu pre vseobecny graf by som potreboval aj ja, s nou by bolo toto zadanie lahko riesitelne. Mozes vyuzit aj vyssie spomenuty dosledok, ale ten ti bude platit len po graf K5, tento kompletny graf uz nie je rovinny.
Ak sa mylim, opravte ma :]
Tymto sa chcem opytat, ci je mozne nejakym sposobom vyuzit tento dosledok aj pre kompletne grafy s v>5.
Dakujem
Offline
#3 02. 12. 2010 16:46
Re: Projekt 3
Zmíněná věta udávající OSTRÝ horní odhad počtu hran v grafu bez trojúhelníků existuje. Její tvrzení a zejména důkaz však jsou nad rámec našeho kurzu. To, co se po vás chce v projektu je výrazně jednodušší. Zatím nikdo neoperoval s nápovědou - použit metodu dvojího počítání.
Co se bude počítat dvěma způsoby?
Offline
#4 03. 12. 2010 12:02
Re: Projekt 3
Nápověda:
metodou dvojího počítání je vhodné použít tak, že dvěma způsoby spočítáme kolik existuje v kompletním grafu různých trojúhelníků  , které obsahují hranu
, které obsahují hranu 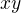 .
.
Tuto nápovědu jsem přidal i na web do zadání projektu.
Offline
#5 03. 12. 2010 12:05 — Editoval Fail (03. 12. 2010 12:06)
Re: Projekt 3
↑ petrkovar:
Dalo by sa postupovat aj inym sposobom bez vyuzitia metody dvojiho pocitani ? Konkretne by som vyuzil kompletne bipartitne grafy. Neviem ci mozem rozpisovat viac aby som neodhalil mozne riesenie.
Dakujem
Offline
#6 03. 12. 2010 12:17
Re: Projekt 3
↑ Fail:Ne každý graf, který splňuje zadání úlohy je bipartitní a proto ani kompletní bipartitní.
Například Petersenův graf neobsahuje trojúhelník, ale není bipartitní. Proto ani řešení založené na argumentaci o úplných bipartitních grafech není správně (není úplné).
Offline
