Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 12. 2010 10:02
Offline
#4 05. 12. 2010 10:39 — Editoval eminich (05. 12. 2010 10:54)
Re: Funkce
tak f:y=0 ani neklesa ani nerastie, je teda konstantna a podla mna je parna(suda) lebo je osovo sumerna podla osy y(, dokazes ku kazdemu x najst -x a je osovo sumerne podla y)
logaritmicka funkcia ma 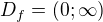
 , zaklad logaritmu nesmie byt 1 a musi byt vacsi ako 0
, zaklad logaritmu nesmie byt 1 a musi byt vacsi ako 0
a 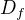 funkcii ktore obsahuju logaritmus, zistis riesenim nerovnic, ako je to v odkaze ktory som poslal
funkcii ktore obsahuju logaritmus, zistis riesenim nerovnic, ako je to v odkaze ktory som poslal
edit: vlastnosti http://oskole.sk/?id_cat=2&clanok=4120
Offline
#9 05. 12. 2010 13:32
Re: Funkce
↑ Datle:
funkce je rostoucí v množině  , jestliže:
, jestliže: 
funkce je klesající v množině  , jestliže:
, jestliže: 
funkce je konstantní, jestliže: 
funkce je neklesající, jestliže 
funkce je nerostoucí, jestliže 
funkce je sudá, jestliže 
funkce je lichá, jestliže 
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
