Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Logaritmicke, exponencialni nerce + abs (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 04. 2008 22:53 — Editoval lopson (25. 04. 2008 23:06)
Logaritmicke, exponencialni nerce + abs
Ahoj,
rád bych se zeptal na něco z teorie. Zajímá mě, jak je to s nerovnicemi exponenciálními a logaritmickými, respektive změna nerovnosti "větší, menší". Mám třeba příklad: , základ je zde menší než 1 a proto se znaménko nerovnosti otáčí na druhou stranu.
, základ je zde menší než 1 a proto se znaménko nerovnosti otáčí na druhou stranu.
V dalším příkladu:
zde je 1/3 také menší než 1 a při dalším řešení se nerovnost také otáčí.
V tomto příkladu: je 1/3 také menší než 1, ale při dalším řešení jsem zjistil, že se zde znaménko neotáčí. Je to tím, že je tam 1/27 tedy číslo menší než 1? Kdyby tam bylo třeba 27 mělo by to jiný vliv na následné řešení? Anebo to ovlivňuje ta absolutní hodnota ??? Hlavně mě právě zajímá tento příklad.
je 1/3 také menší než 1, ale při dalším řešení jsem zjistil, že se zde znaménko neotáčí. Je to tím, že je tam 1/27 tedy číslo menší než 1? Kdyby tam bylo třeba 27 mělo by to jiný vliv na následné řešení? Anebo to ovlivňuje ta absolutní hodnota ??? Hlavně mě právě zajímá tento příklad.
Stačilo by mi to jen nějak jednoduše nastínit, ale abych to hlavně mohl použít na další řešení jiných příkladů.
Díky moc. :-)
Offline
#2 25. 04. 2008 23:00
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Logaritmicke, exponencialni nerce + abs
f rostouci funkce: a<b prave tehdy kdyz f(a)<f(b)
f klesajici funkce: a<b prave tehdy kdyz f(a)>f(b)
pokud na obe strany nerovnice aplikuji klesajici funkci, otoci se znamenko. Nejjednodussi takovy pripad je notoricky zname nasobeni minus jednickou (aplikace funkce y=-x)
Offline
#3 25. 04. 2008 23:04 — Editoval Jorica (25. 04. 2008 23:07)
Re: Logaritmicke, exponencialni nerce + abs
↑ lopson:
Spatne zde pises...nekolikrat...mensi nez nula ;-) Spravne je v intervalu (0; 1).
Kdyz to popisu hodne zjednodusene, souvisi to s tim, zda je funkce rostouci nebo klesajici. Logaritmicka i exponencialni funkce je rostouci, pokud je zaklad logaritmu nebo mocniny vetsi nez 1, pak se nerovnost zachovava. Pokud je ale zaklad v intervalu (0; 1) jedna se o klesajici logaritmickou nebo exponencialni funkci a pri prechodu od logaritmicke ci exponencialni nerovnice ke klasicke nerovnici se otaci znamenko nerovnosti podobne jako pri nasobeni/deleni zapornou hodnotou.
Robert to popisuje presneji...narozdil ode me ;-)
Offline
#5 25. 04. 2008 23:09 — Editoval lopson (25. 04. 2008 23:10)
Re: Logaritmicke, exponencialni nerce + abs
Jop, to jsem věděl, ale jak je to s tím posledním příkladem. Když vlastně na obou stranách jsou čísla menší než 1, chová se to stejně (v řešení), jako by na obou stranách byla čísla větší než 1 ??? --> Tudíž se nemusí otáčet znaménko?
Offline
#6 25. 04. 2008 23:38 — Editoval Jorica (26. 04. 2008 00:04)
Re: Logaritmicke, exponencialni nerce + abs
↑ lopson:
To urcite NE. Preved si to na nasobeni zapornou hodnotou...princip je totiz stejny. O tom, zda otocit ci neotocit znamenko nerovnosti, rozhoduje to, jakym cislem nasobis a ne jaka cisla nasobis?

V obou prikladech budes nasobir hodnotou -1 a proto otocis znamenko nerovnosti....bez ohledu na to, jaka cisla tam byla, zda obe zaporna nebo jen jedno zaporne.
Ve tvem priklade zavisi na tom jaky je zaklad exponencialni fce, to je 1/3, proto se jedna o funkci klesajici a plati: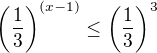
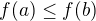 a f je klesajici, proto
a f je klesajici, proto
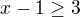
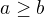
Offline
#7 25. 04. 2008 23:45 — Editoval lopson (25. 04. 2008 23:47)
Re: Logaritmicke, exponencialni nerce + abs
Jopi, no chtěl bych se zeptat na poslední otázku, neřeší prostě vše když ty (1/3 a 1/3 ^3) převedu prostě na 3^-Ix-1I =< 3^-3, to už mi zabezpečí přehození znaménka nerovnosti. Dají se tak řešit všechny exp. nerce? Prostě je takto převézt?
Offline
#13 25. 04. 2008 23:57 — Editoval Jorica (26. 04. 2008 00:16)
Re: Logaritmicke, exponencialni nerce + abs
↑ xificurC:
To mas vlastne pravdu....asi nejvyssi cas jit chrnet, co? :-)
Tak pak autorovi dotazu radim, nejprve rozdelit reseni v intervalech na dve nerovnice tak, aby se zbavil abslutni hodnoty a pak postupovat podle vyse zminenych doporuceni vsech diskutujicich :-))))) A ja jdu spat, zitra si to po sobe prectu a pripadne opravim ty blaboly :-)))
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Logaritmicke, exponencialni nerce + abs (TOTO TÉMA JE VYŘEŠENÉ)