Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 11. 12. 2010 18:48 — Editoval Honza Matika (11. 12. 2010 20:53)
#4 11. 12. 2010 19:50
- VojtechSejkora
- Příspěvky: 176
- Reputace: 5
Re: parabola
↑ rimer:
co třeba takto
teda pokud jsem správně pochopil e potřebuješ oddělat tu 4ku před 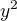
Offline



![kopírovat do textarea $F=\left[3+\frac1{4};0\right]=\left[\frac{13}{4};0\right]$](/mathtex/b0/b03540fcf1906fa1df2e8d075a0b86e8.gif) ?
?![kopírovat do textarea $F=\left[\frac{49}{16};0\right]$](/mathtex/28/282bec5323e13f29c4595bf91b956944.gif)

 ale potom to zase nevychadza podla vysledkov v knihe
ale potom to zase nevychadza podla vysledkov v knihe ![kopírovat do textarea $F=\left[\frac{25}{8};0\right]$](/mathtex/c4/c445218bac044add477650c6b6bc53f3.gif)
![kopírovat do textarea $F[3+\frac1{16};0]$](/mathtex/4d/4d42a3f708dd0a6f6ff8e036b3ab19c8.gif)
 má ohnisko
má ohnisko ![kopírovat do textarea $F[\frac p2;0]$](/mathtex/e5/e582e314e91bd7ca5034a07774087361.gif)