Matematické Fórum

CLieR · 12. 12. 2010 16:59 — Editoval CLieR (12. 12. 2010 17:19)

Zdravím,
rád bych chtěl vidět Váš výsledek na tento příklad. Řešení zanést do jednoho grafu, kdy výsledek je roven sjednocení M1,M2,M3,M4,M5
Žádný obrázek mi nevyšel, jen přímka, parabolka, bod a opět přímka :(

Zadání:
$M1 = (x+2)^2 + (y+1)^2 \leq 4$
$M2 = {|x|\leq1} \wedge y=1+sqrt{|x|}$
$M3 = |x-1|\leq1 \wedge y=-2 + sqrt{|x+1|}$
$M4 = |x-2|\leq1 \wedge y=sqrt{|x-2|}$
$M5 = \frac32 \leq x \leq\frac92 \wedge y \leq-1-|x-4|$

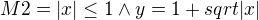
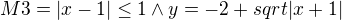
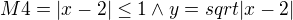
Děkuji :)

EDIT:
Mé výsledky:
jedna parabola
jedna přímka
jedna úsečka
jedna exponenciální
dvě úsečky(spojené, minimum pro y=0 x=2)

CLieR · 12. 12. 2010 17:24

↑ CLieR: Jinak hodněkrát jsem rozděloval na intervaly pro x, kvůli těm absolutním hodnotám, všechno mi vyšlo, jen z toho není obrázek :D

jelena · 12. 12. 2010 17:33

Nepovídej si sam se sebou, prosím, takové téma se zatoulá.

$M1 = (x+2)^2 + (y+1)^2 \leq 4$ vnitřek kruhu - jakého přesně?
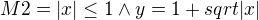$M2 = {|x|\leq1} \wedge y=1+sqrt{|x|}$ vertikální pás a čáry "křídla" odpovídající grafu 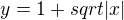$y=1+sqrt{|x|}$ , průníkem jsou jen "křídla"

Žádnou "exponenciální" v zadání nevidím.

Rozdělovat na intervaly není třeba, spíš posouvat.

zbytek už se podaří? Děkuji.

CLieR · 12. 12. 2010 17:40

↑ jelena:
Omlouvám se, měl jsem použít edit..
M1 = vnitřek kruhu? Nechápu.
M2 = ano, "křídla" mi vyšla
M3 = to je právě ta exponenciální (ale jak se na to dívám, nejspíše jsem udělal někde chybu, protože kdybych si dosadil data a pak posunul o 2 "dolů", vyšlo by mi to jinak)
Nemohla by mi to nějaká hodná duše moc prosím alespoň přibližně načrtnout?

jelena · 12. 12. 2010 17:48

↑ CLieR: vyhledej si, prosím, rovnici kružnice (analytická geometrie). Děkuji.

CLieR · 12. 12. 2010 17:52

↑ jelena:
uch, tak jsem si pročetl, chápu, že je to kružnice, která má střed [2,1] a r=2, ale my jsme zatím nepokročili do analytické geometrie, nýbrž nyní začneme řešit věci s goniometrií, nikdo mě v životě neřekl, že existuje rovnice, dle které narýsuji kruh, za tuto informaci Vám velice děkuji :).

jelena · 12. 12. 2010 22:00

↑ CLieR: není za co. Zbytek už není problém?

M3, M4 je stejné jako M2, jen s posunem. M5: vertikální pás v omezeních pro x a část poloroviny pod grafem 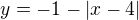$y=-1-|x-4|$

Můžeš označit za vyřešené? Děkuji.

Matematické Fórum

#1 12. 12. 2010 16:59 — Editoval CLieR (12. 12. 2010 17:19)

Máme tu opět obrázek v grafu

#2 12. 12. 2010 17:24

Re: Máme tu opět obrázek v grafu

#3 12. 12. 2010 17:33

Re: Máme tu opět obrázek v grafu

#4 12. 12. 2010 17:40

Re: Máme tu opět obrázek v grafu

#5 12. 12. 2010 17:48

Re: Máme tu opět obrázek v grafu

#6 12. 12. 2010 17:52

Re: Máme tu opět obrázek v grafu

#7 12. 12. 2010 22:00

Re: Máme tu opět obrázek v grafu

Zápatí