Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 12. 2010 19:52
Rovnica
Najdite vsetky riesenia rovnice 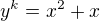 v celych cislach, ked k je prirodzene cislo vacsie ako 1.
v celych cislach, ked k je prirodzene cislo vacsie ako 1.
-
Ked si rovnicu upravim dostanem 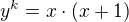 .
.
To znamena, ze  je sucin dvoch po sebe iducich cisel a naozaj sa mi nezda, ze by v takomto pripade existovali ine riesenia ako
je sucin dvoch po sebe iducich cisel a naozaj sa mi nezda, ze by v takomto pripade existovali ine riesenia ako 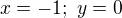 a
a 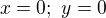 pricom
pricom  moze byt cokolvek. Ako to vsak mam dokazat? Dakujem za pomoc. Slovencina dufam nevadi.
moze byt cokolvek. Ako to vsak mam dokazat? Dakujem za pomoc. Slovencina dufam nevadi.
Offline
- (téma jako vyřešené označil(a) Lancer)
#2 14. 12. 2010 18:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Rovnica
↑ Lancer:
Případy s nulami neřešme, ty už jsi vyřešil.
Na pravé straně je zřejmě kladné číslo. Na levé straně tedy také musí být kladné číslo, což znamená, že k je sudé nebo y je kladné. Pokud je k sudé, pak pokud je nějaké záporné číslo řešením, musí být i číslo k němu opačné řešením. Stačí tedy rovnici řešit pouze pro kladná y a pak pouze v případě sudého k přidat k řešení i čísla opačná.
Podobně stačí najít kladná řešení x a pak k nim přidat hodnoty 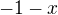 , pro které nabývá
, pro které nabývá 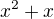 stejné hodnoty.
stejné hodnoty.
Jestliže se nějaké prvočíslo  vyskytuje v prvočíselném rozkladu
vyskytuje v prvočíselném rozkladu  , pak se
, pak se  může vyskytovat pouze v prvočíselném rozkladu jednoho z čísel
může vyskytovat pouze v prvočíselném rozkladu jednoho z čísel  a
a  . Prvočíselný rozklad čísla y tak využijeme k zapsání čísla
. Prvočíselný rozklad čísla y tak využijeme k zapsání čísla  na součin dvou čísel
na součin dvou čísel 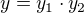 , kde
, kde  je složeno pouze z prvočísel vyskytujících se v prvočíselném rozkladu
je složeno pouze z prvočísel vyskytujících se v prvočíselném rozkladu  a
a  je složeno pouze z prvočísel vyskytujících se v prvočíselném rozkladu
je složeno pouze z prvočísel vyskytujících se v prvočíselném rozkladu  . Je pak jasné, že musí být
. Je pak jasné, že musí být  a
a 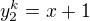 . Odečteme od sebe tyto dvě rovnosti a dostaneme
. Odečteme od sebe tyto dvě rovnosti a dostaneme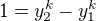
Rozepíšeme pravou stranu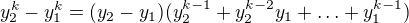 .
.
Obě závorky musí být rovny jedné. Druhá závorka má však alespoň dva členy (k je alespoň dva), přitom oba jsou přirozenými čísly, nelze tedy rovnost splnit. V kladných y tedy rovnice nemá řešení. Nemá ho proto ani v záporných a zbývají tak jen ta nulová řešení.
Offline