Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 17. 12. 2010 16:29
#4 17. 12. 2010 16:40
Re: Inverzní funkce
↑ krabis: zdravim, pouzijeme pravidlo 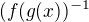 (myslim tym inverznu funkciu k zlozenej neviem ako to inak zapisat)
(myslim tym inverznu funkciu k zlozenej neviem ako to inak zapisat) 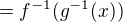 a jednotlive inverzne funkcie:
a jednotlive inverzne funkcie: 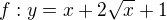
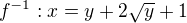
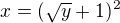
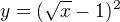 a druha
a druha 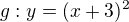
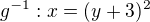
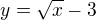 dalej uz len zostavit zlozenu funkciu s tychto dvoch inverznych a dosadit za x 81.
dalej uz len zostavit zlozenu funkciu s tychto dvoch inverznych a dosadit za x 81.
"If you think you understand quantum mechanics, you don't understand quantum mechanics" - Richard Feynman
"Linux is like a tepee no windows, no Gates, apache inside"
Offline
#7 17. 12. 2010 17:17 — Editoval PeetPb (17. 12. 2010 17:20)
Re: Inverzní funkce
↑ krabis: predpis inverznej funkcie by mal byt : 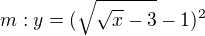 takze vas vysledok je spravny :) ale da sa to upravit
takze vas vysledok je spravny :) ale da sa to upravit 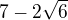
"If you think you understand quantum mechanics, you don't understand quantum mechanics" - Richard Feynman
"Linux is like a tepee no windows, no Gates, apache inside"
Offline
#8 17. 12. 2010 17:17
Re: Inverzní funkce
včera sem počítal téměř stejnej příklad http://www.sdilej.eu/pics/b8b7ba8da923e … 6e18ce.jpg
jenom si místo tý sedmičky dosaď 4
Offline
#9 17. 12. 2010 17:20
Re: Inverzní funkce
↑ roman91:
a posilal si to do moodle, kde to to reklo, ze je to dobre?
Diky
David
Offline


