Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 12. 2010 15:16
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Derivace
Dobrý den, potřebovala bych poradit.
Mám příklad: nalezněte derivaci funkce: y=x.lnx-x
počítala jsem to: podle vzorce (u.v)´= x´. (lnx-x)+x.(lnx-x)´= po úpravě mi vzniklo=1.(lnx-x)+x.(1/x- 1)
po konečné úpravě mi vyšlo lnx-1, ale ve výsledku má vyjít pouze lnx. Nevím, kde mám chybu
Děkuju
Offline
- (téma jako nevyřešené označil(a) lucik.kicul)
#3 20. 12. 2010 15:35
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: Derivace
↑ jelena:
Jestli jsem to pochopila: y=x´.ln(x)-x+ x.ln(x)´-x? Mně se to moc nezdá, ale když mám derivovat x.ln(x), kam se mi podělo -x?
Offline
#4 20. 12. 2010 15:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace
↑ lucik.kicul:
máš to x derivovat také.
Jak derivuješ 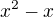 ?
?
Offline
#6 20. 12. 2010 15:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace
↑ lucik.kicul: pěkně derivuješ, děkuji.
přesně ve stejném smyslu derivuj y´=(x.lnx)´-x´ (na závorku platí pravidlo pro součin). V pořádku?
Offline
#8 20. 12. 2010 15:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace
↑ lucik.kicul:
není za co, pokud bys chtěla mít závorky, tak by muselo být vytknuto x takto: x*ln(x)-x=x*(ln(x)-1).
Můžeš označit za vyřešené. Děkuji.
Offline
#9 20. 12. 2010 17:59
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: Derivace
narazila jsem na tento příklad, jsou to také derivace
y=6x+8/16-9x^ 2=počítám dobře?když 6x+8 zderivuji podle derivace sčítání, vyjde mi 6, a ve jmenovateli je vzorec
(4-3x)^ 2, to už mám nechat? nebo se má taky derivovat, potom by mi nevyšel výsledek, který má vyjít 6/(4-3x)^ 2
Offline
#10 20. 12. 2010 22:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace
↑ lucik.kicul:
příště si na nový dotaz založ, prosím, nové téma (a používej správně závorky): y=(6x+8)/(16-9x^2) děrivuješ jako podíl:
děrivuješ jako podíl: 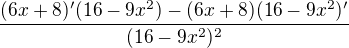
 není totež jako
není totež jako  , k tomu dojdeš až po dalších úpravách (snad) - nezkoušela jsem to, ale stroj to povídá.
, k tomu dojdeš až po dalších úpravách (snad) - nezkoušela jsem to, ale stroj to povídá.
Stačí tak? Děkuji.
Offline