Matematické Fórum

TakyTipek

zdravim, poradi mi niekto prosim Vas, viem ze sucet prevratenych hodnot druhych mocnin je rovny PI na druhu delene 6. Ale nikde v knihach ani na internete neviem najst comu sa rovna tenisty rad akurat na tretiu, stvrdtu, piatu atd. dufam ze chapete .. zle sa to pise na tomto fore ..

jelena · 29. 12. 2010 10:22

TakyTipek napsal(a):
zle sa to pise na tomto fore ..

to myslíš vážně?

Místní možnosti matematických zápisů - viz pravidla + pod oknem zprávy je tlačítko pro vložení obrázku (nouzová situace).

Problému, na který se ptáš, nerozumím, zhruba na 3. klik jsem našla toto. Věřím, že se dostane více použitelného doporučení od odborně zdatných kolegů, děkuji.

Zdravím.

Pavel · 29. 12. 2010 10:28

↑ TakyTipek:

Tvoje otázka úzce souvisí s tzv. Riemannovou zeta funkcí - viz http://en.wikipedia.org/wiki/Riemann_zeta_function

V současnosti umíme v uzavřeném tvaru vyjádřit pouze součty řad se sudými exponenty

$\sum_{n=1}^\infty\frac 1{n^2}=\frac{\pi^2}{6}$

$\sum_{n=1}^\infty\frac 1{n^4}=\frac{\pi^4}{90}$

$\sum_{n=1}^\infty\frac 1{n^6}=\frac{\pi^6}{945}$

$\sum_{n=1}^\infty\frac 1{n^8}=\frac{\pi^8}{9450}$

apod. viz např. zde - http://www.wolframalpha.com/input/?i=su … o+infinity

obecně

$\sum_{n=1}^\infty\frac 1{n^{2m}}=(-1)^{m+1}\frac{B_{2m}(2\pi)^{2m}}{2(2m)!}$

kde $B_m$ jsou tzv. Bernoulliova čísla - viz http://en.wikipedia.org/wiki/Bernoulli_number

Pokud jde o liché exponenty, tak tam součet v uzavřeném tvaru bohužel dodnes neznáme.

TakyTipek

Diki Pavel, Bernoulliova čisla - nemas o nich nieco v slovencine? A akoze sa liche nedaju vyjadrit, to mi tu nechci tvrdit.. kdesi som uz videl aj na tretiu.. ale neviem to znovu zohnat..

Pavel · 29. 12. 2010 11:32 — Editoval Pavel (29. 12. 2010 11:32)

↑ TakyTipek:

Ve slovenštině bohužel nic nemám. Pokud jde o liché exponenty, je to tak, jak říkám. Dosud neumíme součty těchto řad vyjádřit v uzavřeném tvaru pomocí známých konstant $\pi$ , $e$ apod. jako u řad se sudými exponenty.

TakyTipek · 29. 12. 2010 11:47

to je zaujimave ze liche sa nedaju vyjadrit .. urcite sa daju len sa este neprislo nato ako..

teolog · 29. 12. 2010 11:50 — Editoval teolog (29. 12. 2010 11:51)

↑ TakyTipek:
součet dodnes neznáme $=$ dosud neumíme $\neq$ sa nedaju vyjadrit

Ale zajímavé to rozhodně je, s tím souhlasím.

Marian · 29. 12. 2010 14:54 — Editoval Marian (29. 12. 2010 14:54)

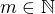↑ Pavel: Snad jen technikcy připomenu, že uzavřený tvar pro $\zeta (2m)$ , $m\in\mathbb{N}$ , se často zapisuje také kratčeji jako

$\zeta (2m)=\frac{|B_{2m}|}{2}\cdot\frac{(2\pi)^{2m}}{(2m)!}.$

Matematické Fórum

#1 29. 12. 2010 09:47 — Editoval TakyTipek (29. 12. 2010 09:48)

konvergentne rady

#2 29. 12. 2010 10:22

Re: konvergentne rady

TakyTipek napsal(a):

#3 29. 12. 2010 10:28

Re: konvergentne rady

#4 29. 12. 2010 11:04 — Editoval TakyTipek (29. 12. 2010 11:09)

Re: konvergentne rady

#5 29. 12. 2010 11:32 — Editoval Pavel (29. 12. 2010 11:32)

Re: konvergentne rady

#6 29. 12. 2010 11:47

Re: konvergentne rady

#7 29. 12. 2010 11:50 — Editoval teolog (29. 12. 2010 11:51)

Re: konvergentne rady

#8 29. 12. 2010 14:54 — Editoval Marian (29. 12. 2010 14:54)

Re: konvergentne rady

Zápatí