Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Singulární matice (důkaz sporem) (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 12. 2010 14:09 — Editoval Azeret (30. 12. 2010 14:55)
Singulární matice (důkaz sporem)
Ahoj mám problém s jedním důkazem (myslím, že tvrzení neplatí, ale můj důkaz říká, že platí).
Mějme tvrzení:  je singulární
je singulární 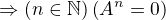 . Ověřte zdalí platí. Předpokládám, tedy, že platí.
. Ověřte zdalí platí. Předpokládám, tedy, že platí.
Důkaz sporem (tedy negace inplikace): 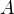 je singulární
je singulární 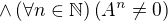 .
.
Tedy stačí nají singulární matici, pro kterou 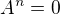 . To je libovolná matice, která má jedničky na vedlejší diagonále nad diagonálou a pak samé nuly,napr:
. To je libovolná matice, která má jedničky na vedlejší diagonále nad diagonálou a pak samé nuly,napr:
,
(to, že pro ni 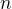 , pro které
, pro které 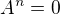 se ověří mat. násobením snadno. To je tedy spor a platí původní implikace.
se ověří mat. násobením snadno. To je tedy spor a platí původní implikace.
Naproti tomu, mějme matici například
,
asi to neumím rigorozne dokázat, ale pokud tuhle matici budu mocnit kolikrát chci, tak to nulu nikdy nedá (pouze se budou zvysovat hodnoty v prvnim a tretim sloupci). Což je ve sporu s původní implikací a někde v důkazu je tedy asi chyba.
Budu vděčná za každou radu, díky.
pi = 3
Offline
- (téma jako vyřešené označil(a) Azeret)
#3 30. 12. 2010 14:36
Re: Singulární matice (důkaz sporem)
Čau,
ty pro spor předpokládáš, že existuje taková singulární matice, pro kterou pravá strana ekvivalence neplatí. Abys tvrzení dokázala, musela bys s tímto předpokladem dojít ke sporu.
Pokud chceš ověřovat, pro které singulární matice pravá strana platí, pro důkaz toho tvrzení to musíš ověřit pro každou.
Tím že jsi našla matici máš protipříklad a tvrzení tedy neplatí.
Mimochodem stačí třeba matice .
Offline
#6 31. 12. 2010 14:27
Re: Singulární matice (důkaz sporem)
↑ FailED:
ja tedy asi nerozumim principu dukazu sporem. Pokud mám implikaci 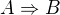 , pak predpoklad pro spor je
, pak predpoklad pro spor je 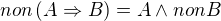 . Tedy s vyrokem
. Tedy s vyrokem  se nic nedeje . . .A proto, kdyz to ma platit pro vsechny singularni matice (to je vyrok A), tak nevim, proc se to pak ''zmeni'' na existuje takove matice . .
se nic nedeje . . .A proto, kdyz to ma platit pro vsechny singularni matice (to je vyrok A), tak nevim, proc se to pak ''zmeni'' na existuje takove matice . .
jinak predem se omlouvam, za sve dlouhe vedeni . .:)
pi = 3
Offline
#8 31. 12. 2010 14:45 — Editoval maly_kaja_hajnejch-Lazov (31. 12. 2010 14:47)
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: Singulární matice (důkaz sporem)
Muj nazor: Takze dokazujeme ze singularnost implikuje nilpotentnost (nejaka mocnina je rovna nulove matici). Sporem to vedeme tak, jak pisete: ze prepokladame, ze matice A je singularni a neni nilpotentni a musime dojit ke sporu. To se dokazuje dost blbe a ve Vasem prispevku jste to neudelal. Tam jste nasel singularni matici ktera nilpotentni je a pak jste nasel jinou singularni matici, ktera nilpotentni neni.
Aspon tak nas to ucil pan ridici v Lazove
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Singulární matice (důkaz sporem) (TOTO TÉMA JE VYŘEŠENÉ)

 , jelikož
, jelikož 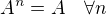
 v tom předpokladu pro spor? Pokud tam, je, pak chápu proč je to špatně.
v tom předpokladu pro spor? Pokud tam, je, pak chápu proč je to špatně.