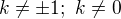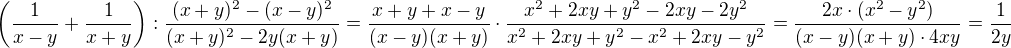Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 11. 2010 09:24
Lomené výrazy
Ahoj všem
Potřeboval bych zkontrolavat pár příkladů.
Příklady 4 ,5 a 7 jsem vypočítal,ale vzhledem k tomu ,že neznám výsledek tak nevím jestli správně a vzhledem k tomu,že jsem si matematikou hrál někdy před 13 rokama tak o tom i dost pochybuji
ten 6 příklad vůbec nevím ja vyřešit a ta 8 ka mi výjde vždy nějak divně :)
Předem děkuji
Offline
- (téma jako vyřešené označil(a) jelena)
#3 26. 11. 2010 11:04
#5 26. 11. 2010 11:38
Re: Lomené výrazy
↑ gadgetka:
Takže to se mnou tak špatný není - moc děkuji za kontrolu a pomoc - jen bych poprosil rozepsat tu 6 ku -páč jsi (jste) tam
použila asi nějaké pravidlo ,které se fakt vykouřilo :)
Offline
#6 26. 11. 2010 11:47 — Editoval gadgetka (26. 11. 2010 11:51)
Re: Lomené výrazy
U té šestky jde o rozklad kvadratického trojčlenu na součin (vyřešíš kořeny kvadratické rovnice a pro rozklad na součin platí 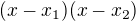 , kde
, kde  jsou kořeny kvadratické rovnice. Zbytek už je jen součet zlomků, čili společný jmenovatel a dopočítání čitatele...Co ty na to, stačí to takto? Teď už to zvládneš?
jsou kořeny kvadratické rovnice. Zbytek už je jen součet zlomků, čili společný jmenovatel a dopočítání čitatele...Co ty na to, stačí to takto? Teď už to zvládneš?
Např.: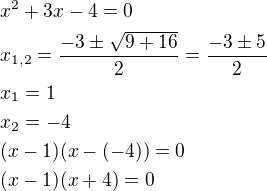
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#7 26. 11. 2010 11:58
Re: Lomené výrazy
↑ gadgetka:
bohužel tápu - nevím přesně jak jsi to rozložila - AX(na druhou)+BY+C = 0 - teda jestli mi to alespon něco říká ,ale vůbec nevím jak - chtěl bych to pochopit
Offline
#10 26. 11. 2010 12:03
Re: Lomené výrazy
↑ gadgetka:
Aha - mě se tam předtím nezobrazil ten obrázek - takže jsi u každého z nich vypočítala kořeny přes diskriminant a dosadila do to toho? v závislosti na tom pravidle 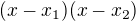
Offline
#12 26. 11. 2010 12:06
#14 26. 11. 2010 12:25
Re: Lomené výrazy
↑ gadgetka:
jen bych se ještě zeptal - hledal jsem toto na internetu a dobral jsem se,že by měla být rovnice zapsána
takhle a(x - x1)(x - x2) = 0 -to je ono ? je to o tom ,že naše A je jednička ale jinak je to ono ?
zdroj http://cs.wikipedia.org/wiki/Kvadratick%C3%A1_rovnice
Offline
#15 26. 11. 2010 18:23 — Editoval gadgetka (26. 11. 2010 18:24)
Re: Lomené výrazy
Nevím, jak kloudně na tuto otázku odpovědět. Pokud je 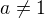 [různé od 1], pak se může celá kvadratická rovnice vydělit členem
[různé od 1], pak se může celá kvadratická rovnice vydělit členem  a dostaneš
a dostaneš 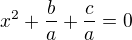 a když označíš
a když označíš 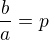 a
a 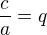 , vzniká ti tzv. normovaný tvar kvadratické rovnice, pro jehož kořeny opět platí
, vzniká ti tzv. normovaný tvar kvadratické rovnice, pro jehož kořeny opět platí  a
a  . Takže jsi opět u toho, že
. Takže jsi opět u toho, že 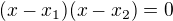 . A pokud vypočítáš kořeny kvadratické rovnice podle vzorce
. A pokud vypočítáš kořeny kvadratické rovnice podle vzorce 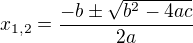 , myslím si, že je úplně zbytečné si pamatovat, že když je D>0, pak se dá rovnice zapsat ve tvaru
, myslím si, že je úplně zbytečné si pamatovat, že když je D>0, pak se dá rovnice zapsat ve tvaru 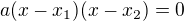 . Podle mne by to možná bylo platné v nějakém příkladu, kde bys měl pomocí kořenů a členu
. Podle mne by to možná bylo platné v nějakém příkladu, kde bys měl pomocí kořenů a členu  sestavit kvadratickou rovnici, ale při rozkladu trojčlenu na součin, je to úplně zbytečná informace, která ti v mozku zabere místo pro nějakou daleko důležitější věc. :) Ale názory kolegů se pochopitelně mohou lišit. :D
sestavit kvadratickou rovnici, ale při rozkladu trojčlenu na součin, je to úplně zbytečná informace, která ti v mozku zabere místo pro nějakou daleko důležitější věc. :) Ale názory kolegů se pochopitelně mohou lišit. :D
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#16 03. 01. 2011 18:49
Re: Lomené výrazy
Dobrý den, prosím o pomoc, nevím jak mám vypočítat tento příklad, pomůže mi někdo? :)
{1} {x - 2a} + {1} {x + 2a} + {8a^2} {4a^2 * x - x^3}
(1/x-2a) + (1/x+2a) + (8a^2/4a^2*x-x^3)
V tom TeXu se moc nevyznám, raději jsem to napsala 2x. Doufám, že to bude nějak k pochopení :)
Offline
#17 03. 01. 2011 21:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lomené výrazy
↑ Terinka.J:
Zdravím, příště si založ samostatné téma na svůj dotaz. Děkuji.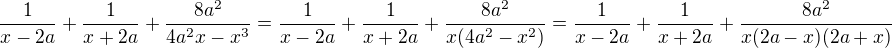
v posledním zlomku jsem nejdřív vytkla x a závorku jsem rozložila podle vzorce  . Abych našla společný jmenovatel, musím před 1. zlomek vytknout (-1).
. Abych našla společný jmenovatel, musím před 1. zlomek vytknout (-1).
Už se podaří? Děkuji.
Offline
#18 04. 01. 2011 23:57
Re: Lomené výrazy
↑ Terinka.J: Je výsledek 2 lomeno X ?
Je mi 49 a studuji cao8 dálkově, 1. ročník, jsem osvč-kadeřnice. Matematika mne, kupodivu, baví:)
Offline
#19 05. 01. 2011 00:06
#20 05. 01. 2011 00:29
Re: Lomené výrazy
↑ Honza Matika: Děkuji dnes mám zkoušku, tak počítám, co se dá:)
Je mi 49 a studuji cao8 dálkově, 1. ročník, jsem osvč-kadeřnice. Matematika mne, kupodivu, baví:)
Offline

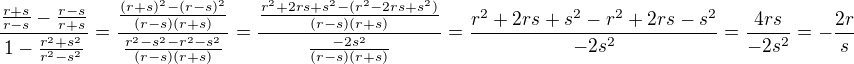
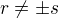
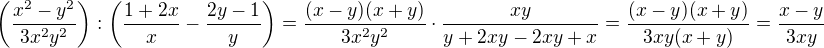
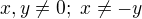

 + podmímky
+ podmímky