Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 03. 01. 2011 16:45 — Editoval Cheop (03. 01. 2011 16:52)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Tečna k parabole
↑↑ georgeo4:
Rovnice přímky rovnoběžné s přímkou p bude mít tvar: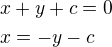 toto dosadíme do rovnice kuželosečky tedy:
toto dosadíme do rovnice kuželosečky tedy: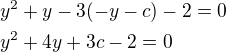 aby přímka měla s kuželosečkou jeden společný bod
aby přímka měla s kuželosečkou jeden společný bod
potom diskriminant této kvadratické rovnice musí být 0 tj: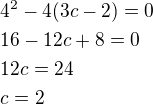
Rovnice tečny: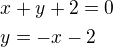
Obrázek:
Nikdo není dokonalý
Offline
#3 03. 01. 2011 17:06
Re: Tečna k parabole
Děkuji moc já došel k diskriminantu a počítal jako diskriminant ne že se to má rovnat 0 dík
Kdybyste byl někdo tak hodný mohli byste prosím ještě zkusit vypočítat tohle díky :
1)Určete odchylku tečen, které lze sestrojit z bodu M[0;-2] k parabole x^2 - 8y = 0 výsledek 90 stupňů
2)Napište rovnici tečny paraboly tak, aby odchylka tečny a osy x byla 45stupňů parabola y^2 +4x - 8 výsledek y = -x + 3
Začnu skoro vždy dobře ale nikdy se mi to nepodaří dokončit do přesného výsledku díky :-)
Offline
#4 03. 01. 2011 18:32
Re: Tečna k parabole
↑ georgeo4:
přímka procházející bodem ![kopírovat do textarea $M[0;-2]$](/mathtex/0b/0b4ff6c9d1a0187da59790060af82c19.gif) má rovnici
má rovnici 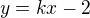 . Dosazením do rovnice paraboly dostaneme
. Dosazením do rovnice paraboly dostaneme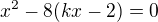
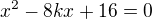
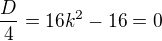
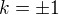
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 03. 01. 2011 19:12
Re: Tečna k parabole
↑ zdenek1:
přesně sem jsem taky došel akorát že já z toho 16k^2 -16 a k1 a k2 mi vyšlo úplně jiné než vám ale i kdyby to tak vyšlo tak jak z toho zjistím tu odchylku je nějáký vzoreček tangens fí = k1-k2/ 1+ k1*k2 v absolutní hodnotě ale nevím mě vyšlo k1=-4 a k2=8k-8 já ten D nekrátil . :-)
Offline
#6 03. 01. 2011 22:07
Re: Tečna k parabole
↑ georgeo4: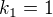 ,
, 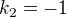
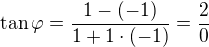 není definován.
není definován.
Pro jaký úhel není tangens definován?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 03. 01. 2011 22:19
Re: Tečna k parabole
↑ zdenek1:
jejda už sem si toho všiml co jsem udělal blbě a přitom taková hloupost dík moc :-)
Offline