Matematické Fórum

Vlastik · 04. 05. 2008 10:31

zdravím, jsem v koncích s těmito dvěma příklady, mohl bych někoho z vás poprosit o řešení ? díky

--------------------------------------------------------------
Součet 1. a 18. sčítance na levé straně rovnice x+3x+5x+...+51x = 3380
je roven ? Výsledkem by mělo být číslo 180.
--------------------------------------------------------------
Součet všech čísel, která vyhovují nerovnici x^2 - 101x + 198=<0
a jsou dělitelná čtyřmi, je roven ? Výsledkem by mělo být číslo 1200.
--------------------------------------------------------------
=< (menší nebo rovno)

plisna · 04. 05. 2008 10:53

k tomu prvnimu:

jde o aritmetickou posloupnost parametry 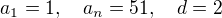$a_1 = 1, \quad a_n = 51, \quad d = 2$

abychom mohli rovnici vyresit, potrebujeme tu posloupnost na leve strane rovnice secist pomoci gaussova vzorce 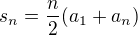$s_n = \frac{n}{2}(a_1+a_n)$ , ale k secteni te posloupnosti potrebujeme vedet pocet clenu $n$ , ktery spocteme z $a_n = a_1 + (n-1)d \qquad \Rightarrow \qquad 51 = 1 + 2(n-1) \qquad \Rightarrow \qquad n = 26$ .

pak rovnici upravime na 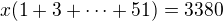$x(1+3+\dots+51) = 3380$ , kde $1+3+\dots+51 = \frac{26}{2}(1+51) = 676$ .

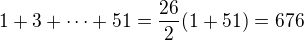dostali jsme tedy rovnici 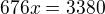$676x = 3380$ , jejiz resenim je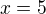 $x=5$

nyni staci vzit prvni a 18. scitanec, vynasobit je 5 a secist.

prvni scitanec je 1, tedy prvni clen je 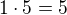$1 \cdot 5 = 5$
18. scitanec je 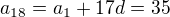$a_{18} = a_1 + 17d = 35$ , tedy 18. clen je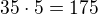 $35 \cdot 5 = 175$

kdyz je oba secteme, dostaneme 5 + 175 = 180

halogan

Edit: opět pomalejší :)

1)
Zjistime, jake je x. Je tam 26 clenu, takze:
$\frac{n}{2}(a_1 + a_{26}) = 13 (x + 51x) = 3380$
z toho vychazi x = 5.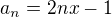

$a_n = 2nx - 1$
z toho vychazi, ze 18. clen je 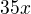$35x$

a 35*5 + 5 = 180

2)
Vyjdou kořeny 2 a 99. Mezi nimi je to menší rovno nule.

Vytvoříme posloupnost násobků 4.
$a_1 = 4 \nl d = 4 \nl a_n = 96 = a_1 + d(n-1) \nl a_{24} = 96 \nl$

Přes vzorec pro ntý člen jsem zjistil, kolikátý člen je 96 (člen poslední) a můžu pak použít vzorec pro součet:
$s_n = \frac{n}{2}(a_1 + a_n) = 12 (4 + 96) = 1200$

jelena · 04. 05. 2008 10:55 — Editoval jelena (04. 05. 2008 10:57)

↑ Vlastik:

Zdravim :-)

neni duvodu byt v koncich

zadani 1. podivej, jak se tvori soucet v prvni priklade (leva strana rovnice) - cisla pred x:
1, 3, 5, 7, 9 .... uz vidis?
ted bud na prstech (vazne) se dopocitam jake cislo bude pred 18. clenem - (je to cislo 35?)
nebo cislo pred 18. clenem odhadnu, jak se vytvari: - zkus to uhadnout - pokud scitanec bude stat na nejakem poradi n, jak se vypocte jeho koeficient (to je to cislo pred x).
Jeste je jeden figl - pokud sectes cisla pred prvnim a poslednim scitancem, pred druhym a pred poslednim ... dostates vzdy stejne cislo 52 - to vyuzijeme take.

zadani 2. Nejdriv najdi interval, pro ktery plati nerovnice - je to kvadraticke nerovnice, najdes koreny rovnice, dal lze resit graficky. Pak muzeme pocitat opet na prstech (on ten interval nebude nejak moc dlouhy), ale jednodussi bude najit prvni a posledni clen a vytvorit si vzorecek pro kazdy nasledujici clen a pak najit jejich soucet. OK?

Ozvi se tady, za se to povedlo, pokud to nepujde, napisi kompletni postup.

Editace: Zdravim, kolegove :-) to jsem rada, ze nas kolega Vlastik uz nebude v koncich - prenechavam vasemu dohledu :-)

Jorica · 04. 05. 2008 10:58 — Editoval Jorica (04. 05. 2008 11:00)

↑ Vlastik:
Opakovani je sice matka moudrosti, ale v tomto pripade uz by bylo zbytecne :)

plisna · 04. 05. 2008 11:00 — Editoval plisna (04. 05. 2008 11:01)

k tomu druhemu:

resenim nerovnice 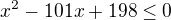$x^2-101x+198 \leq 0$ je interval 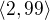$\langle 2, 99 \rangle$ . staci tedy najit v tomto intervalu nejmensi a nejvetsi cele cislo delitelne 4 a sestavit z nich aritmetickou posloupnost.

nejmensi cislo delitelne 4 je 4
nejvetsi cislo delitelne 4 je 96

mame tedy aritmetickou posloupnost s parametry 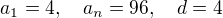$a_1 = 4, \quad a_n = 96, \quad d=4$ .
nyni uz staci nalezt pocet clenu teto posloupnosti a opet pres gaussuv vzorec je secist.

opet vyjdeme ze vztahu 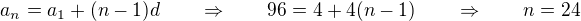$a_n = a_1 + (n-1)d \qquad \Rightarrow \qquad 96 = 4 + 4(n-1) \qquad \Rightarrow \qquad n = 24$

pak soucet vsech cisel z vyse uvedeneho intervalu delitelnych 4 je 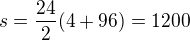$s = \frac{24}{2}(4+96) = 1200$

EDIT: uups, posledni :)