Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 05. 2008 15:27
Lokální extrémy
Ještě jsem našel jeden příkladík se kterým mám menší problém. Výsledky mám, poněvadž jsem si nakreslil graf, ale početně nevím jak to vyřešit
Zadání:
Najděte všechny lokální extrémy 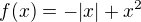
No snažil jsem se to vyřešit tak, že pro x>0; x=0; x<0 ale nějak jsem nedošel k tomu k čemu bych chtěl, nebo nevím jak to zapsat
Offline
#2 04. 05. 2008 15:51 — Editoval jelena (04. 05. 2008 15:52)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální extrémy
↑ NetFenix:
Toto jen napad:
Ja bych udelala 2 funkce - odstranim absolutni hodnotu:
pro interval (-oo, 0) budeme 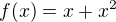 a na tomto intervalu bych poresila (tady mi vychazi bod podezrely z exteremu -0,5) a obdobny postup pro interval od 0 do + oo. Overim, zda to jsou extremy a, pokud ano, tak o jake extremy se jedna. Jeste bych se podivala, co se deje v bode (0,0) - asi pomoci limity zleva a zprava.
a na tomto intervalu bych poresila (tady mi vychazi bod podezrely z exteremu -0,5) a obdobny postup pro interval od 0 do + oo. Overim, zda to jsou extremy a, pokud ano, tak o jake extremy se jedna. Jeste bych se podivala, co se deje v bode (0,0) - asi pomoci limity zleva a zprava.
OK?
Offline
#3 04. 05. 2008 15:52
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Lokální extrémy
x>0 x^2-x to je jednoduché, protože to je parabola
x<0 funkce je sudá takže ze symetrie, využít předchozího
x=0 tady funkce nem0 derivaci, takže asi podle obrázku.
Offline
#4 04. 05. 2008 15:53
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Lokální extrémy
↑ jelena:
Pěkné nedělní odpoledne :). Ta limita toho v nule moc neřekne, spíš derivace zleva a zprava. Ale ten obrázek je jednodušší.
Offline
#5 04. 05. 2008 15:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální extrémy
↑ robert.marik:
Take Vas zdravim :-) urcite mate pravdu (take bych pouzila obrazek, byl to spis takovy rychly dovetek k bodu (0,0) aby uplne nevymizel z pozornosti :-)
Offline
#7 04. 05. 2008 17:08 — Editoval jelena (04. 05. 2008 23:47)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální extrémy
↑ NetFenix:
Pokud tomu rozumim dobre, tak hodnoty -0,5, +0,5 jsi nasel po "polození 1. derivace 0". Ted overujes, zda nastala zmena znamenka derivace pred -0,5 a hned po nem (treba dosazenim -1 a -0,25) do vyrazu pro prvni derivaci na tomto intervalu.
A stejne postupujes pro hodnotu 0,5 a druhi interval (nebo muzes to overovat nalezenim 2. derivace v bodech -0,5 a 0,5 - jak mas vice zazito).
Dle meho jsou to minima a v bode (0,0) derivace neexistuje - je to videt z grafu (nejsem si jista s odbornym nazvem toho utvaru, co vznikl na grafu v bode 0,0 :-)
OK?
Edit: formulace k bodu (0,0) je konzultovana v dalsich prispevcich
Offline
#9 04. 05. 2008 19:01
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Lokální extrémy
↑ jelena:
ja myslim ze to je lokalni maximum. v okoli jsou jenom mensi funkcni hodnoty, funkc se meni z rostouci na klesajici
jmeno taky nevim, bod vratu to neni, mozna uhlovy bod?
Offline
#10 04. 05. 2008 20:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální extrémy
↑ robert.marik:
Omlouvam se za zmatek - mela jsem na mysli, ze - derivace v bode 0 zleva je +1, derivace zprava je -1 - tedy derivace v bode neexistuje, ale lokalni max to je. Je to lepsi formulace?
Offline
#11 04. 05. 2008 21:11 — Editoval robert.marik (04. 05. 2008 21:11)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Lokální extrémy
Je to dokonce dokonala formulace :)
Takovy bod ma urcite nejaky nazev, mozna to bude ve starsich sktiptech na technice, treba Tomica. Ja ten jejich pristup (davat nazvy vsemu co vidim) moc nemusim, takze nemuzu na 100 procent rict, ze to je ten uhlovy bod. ale asi jo http://cs.wikipedia.org/wiki/Uzel_k%C5%99ivky
Offline
#13 05. 05. 2008 21:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Lokální extrémy
↑ robert.marik:
Kdo rekl, ze to je hrot? :-)
Offline
#14 05. 05. 2008 21:20
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Lokální extrémy
:)
to ale neni mysleno jako terminus technikus, jako nazev toho bodu.
Ale rozesmalo me to :)
Offline