Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti {a_n} vs. konvergence řady (TOTO TÉMA JE VYŘEŠENÉ)
#2 08. 01. 2011 10:32 — Editoval jarrro (08. 01. 2011 10:41)
Re: Vlastnosti {a_n} vs. konvergence řady
tak ak rad absolutne koverguje tak a_n sa blíži k nule a ešte to delíš veľkým číslom tak sa to bude ešte skôr blížiť k nule
opačne to neplatí,lebo stačí zobrať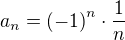
v druhej úlohe ak a_n sa blíži k nule tak 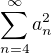 nemusí konvergovať
nemusí konvergovať
stačí zobrať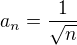
naopak to platí,lebo ak rad konverguje tak 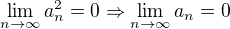
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti {a_n} vs. konvergence řady (TOTO TÉMA JE VYŘEŠENÉ)