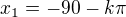Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 09. 01. 2011 13:14 — Editoval CLieR (09. 01. 2011 13:20)
Re: Goniometrické rovnice II.
↑ BakyX:
Jakto?
Není to 180 + 45 = 225 =  ?
?
V tom případě nevím, jak to zjistit :(, napadá mě snad jen 315?
EDIT:
Nejspíše jsem špatně pochopil jednotkovou kružnici.....
najdu si kolmici na ose x pro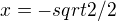 , vytvoří se mi dva průsečíky, a to
, vytvoří se mi dva průsečíky, a to 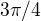 a
a  , ale asi, když mám špatně druhý kořen, tak kořeny budou
, ale asi, když mám špatně druhý kořen, tak kořeny budou 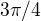 a
a 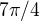 , je to tak? I kdybych vzal v úvahu tyto dva kořeny, stejně mi zpětná substituce nevyjde ....
, je to tak? I kdybych vzal v úvahu tyto dva kořeny, stejně mi zpětná substituce nevyjde ....
Offline



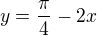 (to je ta substituce)
(to je ta substituce)