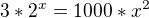Matematické Fórum

↑ marekjanu:

zdravim :-)

Ta rovnice, jak je napsana, reseni ma (dokonce 2 reseni), ale bud se musi resit graficky nebo numericky - hledani priblizne hodnoty - ktera vychyzi priblizne +/- 0,055 (takovy hruby odhad). Je to zadani urcite v poradku?

A pokud neni tajne, odkud je zadani?

Zdravim kolegu thriller :-) vidim, ze mame stejny nazor - ja jsem vychazela z toho, ze je to hodne blizko 0, tedy 2^x temer 1. Tak jsem zkusila odmocninu z 3/1000 - levou cast paraboly jsem neresila, mas pravdu, bude o neco maaaaalo bliz k ose y.

Pokud nepouzivam zadnou numerickou metodu: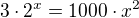

  v teto uprave si nakreslim graf, ze ktereho je zrema velmi uzka parabola, ktera se krizi s exponencialni funkci velice blizko osy y.

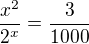pak ta moje uvaha o prispevek vys:

2^x velmi blizko osy y je temer 1,  v podstate resim x^2 = 3/1000

Je to ovsem hodne polopaticky a zjednoduseny postup, ale velmi dobre funguje pro odhady a kontrolu vysledku.

Je mozne pouzit samozrejme neco z numerickych metod, ale to je trochu nuda.

Ahoj, tak zadání mám ze školy - přišla s tím jedna moje spolužačka, že to bylo v ukázkových přijímačkách snad na VŠE, a že s tím nemůže hnout. Pravděpodobně se jedná o nějakou chybu v zadání.

Zkoušel jsem to řešit v Excelu, nechal jsem si vykreslit graf a stále dosazoval přesnější hodnoty.
Výsledky mám dva: x=-0,53761 a x=16,46316 Mohl bych to vyčíslit ještě mnohem přesněji, ale to je nuda bez jakéhokoli tvůrčího postupu.

Jeden člověk na jiném fóru napsal:"Jak je vidět, "hezké" (celočíselné) řešení neexistuje - pravá strana je dělitelná 5, levá ne; reálné řešení dá Lambertova W-funkce: http://en.wikipedia.org/wiki/Lambert_w_ … ons".

Našel jsem trochu podobný případ: http://mathforum.org/library/drmath/view/54607.html (uvádí řešení jako převést si to na funkci a hledat, kdy je funkce rovna 0)

K tomu, abych mohl říct, jak to řešit, nemám bohužel potřebné znalosti, možná by šlo tohle: http://cs.wikipedia.org/wiki/Metoda_te%C4%8Den