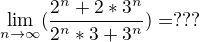Matematické Fórum

Reshi · 09. 01. 2011 19:43 — Editoval Reshi (09. 01. 2011 19:47)

zdravim prosim vas uz celkom hodnu chvilu rozmyslam nad tym ako poriesit nasledujucu limitu:
$\lim_{n\rightarrow\infty} ( \frac {2^n+2*3^n} {2^n*3+3^n})= ???$

Diki :)

teolog · 09. 01. 2011 19:46 — Editoval teolog (09. 01. 2011 19:46)

↑ Reshi:
Také zdravím,
x se blíží k nekonečnu, ale výraz vůbec x neobsahuje. Neplatí to spíš pro n?

Reshi · 09. 01. 2011 19:47

och ano ospravedlnujem sa hned prepisem

PeterSheldon · 09. 01. 2011 22:17

↑ Reshi:

tento příklad není vůbec těžký.. stačí jen vhodně vytknout. Je nutné si uvědomit, co budeš vytýkat. Pokud bychom vytkli 2^n dostali bychom se pak k výrazu nekonečno / nekonečnem, což není dobře.

úprava je následující:

poslední krokem je, že v čitateli a jmenovateli se zkrátí 3^n. Pak je zřejmé, že (2/3)^n (jde-li n-> nekonečna) pak celý výraz jde k 0 .. ve výsledku tedy dostaneš 2/1 tudíž výsledek je 2.

Reshi · 10. 01. 2011 12:35

jasne dakujem velmi pekne :) inak tak som to aj spravil raz len som nevidel to riesenie hentak hned :)

Matematické Fórum

#1 09. 01. 2011 19:43 — Editoval Reshi (09. 01. 2011 19:47)

Limita

#2 09. 01. 2011 19:46 — Editoval teolog (09. 01. 2011 19:46)

Re: Limita

#3 09. 01. 2011 19:47

Re: Limita

#4 09. 01. 2011 22:17

Re: Limita

#5 10. 01. 2011 12:35

Re: Limita

Zápatí