Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 03. 05. 2008 18:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometricka rovnice
↑ ravien:
zdravim - ma to byt reseno na nejakem intervalu?
Prvni vysledek je videt z vlastnosti funkce tg: rovnice ma reseni pro x = 0.
Dalsi vysledky bych hledala spise graficky.
Offline
#4 04. 05. 2008 19:57
Re: goniometricka rovnice
↑ kontinual:Stačí to takto ? : 
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#6 04. 05. 2008 21:04
Re: goniometricka rovnice
↑ kontinual: vynasobim -1
vynasobim -1

Zavedla bych substituci t=2x no a dal uz by to nemusel byt tak velky problem, kdyztak se ozvi.
Offline
#7 05. 05. 2008 06:57
Re: goniometricka rovnice
↑ kontinual:↑ Jorica:Oba zdravím , já bych to řešila takto : Co je tedy správnější ?
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#8 05. 05. 2008 11:02
Re: goniometricka rovnice
↑ Ivana:
Diky za "hozeni na papir", vcera uz z me strany nejak nebyla sila ;)
Jen neodpovidaji reseni Tvym a mym postupem, opomenla jsi podelit v zaveru 2 i periodu 2*k*pi, takze by vysledek mel vypadat takto: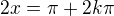 delim 2
delim 2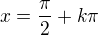
Tvoje dva vysledky je daji zapsat do jednoho prave stejnym zapisem. Vim, ze z tve strany to byl preklep, ja jen aby to nematlo toho, kdo pokladal dotaz ;)
Offline
#11 06. 05. 2008 06:49
Re: goniometricka rovnice
↑ kontinual:Zdravím a pořád platí , že chybami se člověk učí a to po celý život . Hodně zdaru při počítání . :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline

 =
= 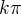 . :-)
. :-)