Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 01. 2011 16:11
Inverzní fce
Zdravim, prosim o pomoc pri reseni prikladu. Mam zadanu funkci f(x)=(a^x + a^-x)/2 a mam algebraicky zjistit jak vypada inverzní fuknkce, sedel jsem nad tím dlouho a porad ne a ne se dobrat vysledku... díky mo za odpoved.
Offline
- (téma jako vyřešené označil(a) 007jirka)
#3 07. 01. 2011 16:26
Re: Inverzní fce
↑ Rumburak: problemem je ze metodu vím, ale porád mi tento príklad nechce vyjít...
Offline
#4 07. 01. 2011 16:45
Re: Inverzní fce
↑ 007jirka:
Tak sem napiš svůj postup, ať zjistíme, kde je chyba - tak se to naučíš nejlíp.
Já se na forum znovu dostanu až v pondělí, takže pravděpodobně Ti to dříve zkontroluje někdo jiný.
Offline
#6 09. 01. 2011 19:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inverzní fce
↑ 007jirka: to se mi nezdá, že by z tohoto doporučení vzniklo t=+/-1 (navíc vážený kolega ↑ Rumburak: bude těžko vědět, co znamená taková substituce).
Ale samozřejmě - záleží jen na Tobě, zda chceš umístit nebo neumístit svůj postup. Problém inverzních funkcí netiží ani mne, ani váženého kolegu, kterého takto srdečně zdravím.
Offline
#7 10. 01. 2011 10:50
Re: Inverzní fce
dle rady jsem si za a^x zavedl substituci t ... z toho dostanu y=1/2 *t *(1+1/t^2) ... vcera mi vyslo zminene t +- 1 , dnes po dalsim pokusu jiz 0 a 1 vim ze je to spatne ale i kdyby ne tak mi neleze do hlavy jak z toho vytriskam x=.... . Kdyz jsem pocital jine priklady tak vse slo v poradku ale jakmile se objevi cokoliv s x v exponentu tak v tom zacnu mit chaos.
Offline
#9 10. 01. 2011 11:37
Re: Inverzní fce
↑ 007jirka:
Shodli jsme se, že jde o to vyřešit rovnici
(1) 
v závislosti na parametru  , kde
, kde  . Tedy i funkce
. Tedy i funkce  je závislá na parametru, a sice na parametru
je závislá na parametru, a sice na parametru  .
.
Máme tady, po rozepsání, řešit rovnici

závislou na dvou parametrech  .
.
Výhodnější ale bude nejprve se zamyslet nad tím, jak je funkce  poskládána, a využít toho. Označíme-li
poskládána, a využít toho. Označíme-li
 ,
, 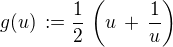
vidíme, že platí  , neboli
, neboli 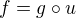 . Máme tedy řešit rovnici
. Máme tedy řešit rovnici  . Tvar levé strany nám umožňuje
. Tvar levé strany nám umožňuje
rozdělit úlohu do dvou jednodušších kroků :
I. Vyřešit rovnici  v závislosti na parametru
v závislosti na parametru  (po úpravě to bude kvadratická rovnice),
(po úpravě to bude kvadratická rovnice),
II. Vyřešit (exponenciální) rovnici  v závislosti na
v závislosti na  , kde
, kde  je řešení rovnice
je řešení rovnice  z kroku I.
z kroku I.
Tato úvaha je nespíše podstatou té substituce, kterou navrhli kamarádi.
PS. S radostí opětuji pozdrav milé a vážené kolegyni Jeleně .
Offline
#11 10. 01. 2011 11:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inverzní fce
↑ 007jirka:
myslím, že žádná vlastnost logaritmů neumožňuje rozepsat ani ten "první logaritmus", natož ten "poslední".
Bude lepší, když ponechaš x=log(.....)
↑ Rumburak: děkuji za podrobný a přehledný výklad a za pozdrav, také opětuji :-)
Offline
#14 10. 01. 2011 12:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Inverzní fce
↑ 007jirka: smekám před podrobným a přehledným výkladem kolegy ↑ Rumburaka:,
teď si ovšem nevzpomínám, zda jsme hovořili o podmínce, že funkce f(x) měla být prostá - pro nalezení inverzní funkce musíme ještě určit interval, na kterém je prostá. A také diskusi parametru  jsme neprovedli.
jsme neprovedli.
A už nevím, na ce jsme se ještě neohledli :-) Spolehám na váženého kolegu, děkuji.
---------------------------
...
Offline
#15 10. 01. 2011 15:23 — Editoval Rumburak (10. 01. 2011 16:30)
Re: Inverzní fce
↑ 007jirka: Je potřeba neunáhlit se a postupovat s rozmyslem, rozhodně ne mechanicky. Uvědomme si nejprve základní vlastnosti
uvažovaných funkcí, tím situaci budeme moci zjednodušit pomocí vhodných doplňujících předpokladů.
Máme-li za funkci  považovat reálnou funkci, jejímž definičním oborem je množina všech reálných čísel, musíme předpokládat
považovat reálnou funkci, jejímž definičním oborem je množina všech reálných čísel, musíme předpokládat  .
.
Funkce  pak nabývá pouze kladných hodnot . Dále: je-li
pak nabývá pouze kladných hodnot . Dále: je-li  , potom i
, potom i  .
.
Takže rovněž funkce  nabývá pouze kladných hodnot. Zároveň připojme předpoklad
nabývá pouze kladných hodnot. Zároveň připojme předpoklad  , tím vyloučíme případ, kdy funkce
, tím vyloučíme případ, kdy funkce  a
a
tedy i  jsou konstantní - pak by totiž inversní funkce zcela jistě neexistovala.
jsou konstantní - pak by totiž inversní funkce zcela jistě neexistovala.
I. V rovnici  dle ↑ Rumburak: se tedy můžeme omezit na
dle ↑ Rumburak: se tedy můžeme omezit na  , aniž bychom tím o něco přišli.
, aniž bychom tím o něco přišli.
Při tomto předpokladu kvadratická rovnice  vzniklá úpravou rovnice
vzniklá úpravou rovnice  má nezáporný diskriminant
má nezáporný diskriminant
(a tedy reálné kořeny) právě když  . Ony reálné kořeny zmíněné rovnice pak budou
. Ony reálné kořeny zmíněné rovnice pak budou  .
.
Tímto máme vyřešen krok I, za  z kroku II pak bereme postupně čísla
z kroku II pak bereme postupně čísla  .
.
Nyní proveďme krok II. Tento krok se opět rozpadne na dva případy podle volby  :
:
1)  .
.
Rovnice  má v tomto případě tvar
má v tomto případě tvar  (na pravé straně je kladné číslo) a tedy jediné řešení
(na pravé straně je kladné číslo) a tedy jediné řešení  .
.
2)  .
.
Rovnice  má v tomto případě tvar
má v tomto případě tvar 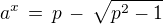 (na pravé straně je opět kladné číslo) a tedy jediné řešení
(na pravé straně je opět kladné číslo) a tedy jediné řešení  .
.
Pro  je
je  . Pro
. Pro  se kořeny
se kořeny  liší , splňují však vztahy
liší , splňují však vztahy  (neboť
(neboť  )
)
a dále  v případě
v případě  resp.
resp.  v případě
v případě  .
.
Za předpokladů  ,
,  jsme tedy ukázali:
jsme tedy ukázali:
Rovnice  je řešitelná pouze pro
je řešitelná pouze pro 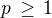 , tedy oborem hodnot fce
, tedy oborem hodnot fce  je interval
je interval  .
.
Řešení však je jednoznačně určeno pouze v případě 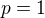 , v případě
, v případě  existují řešení dvě, z nichž jedno je kladné a druhé záporné.
existují řešení dvě, z nichž jedno je kladné a druhé záporné.
Funkce  proto NENÍ prostá v
proto NENÍ prostá v  a tedy NEMÁ inversní funkci.
a tedy NEMÁ inversní funkci.
Avšak označíme-li 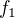 zúžení funkce
zúžení funkce  na interval
na interval  , potom funkce
, potom funkce 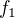 už prostá je a k ní inversní je buďto
už prostá je a k ní inversní je buďto  ,
,  v případě
v případě  nebo
nebo ,
,  v případě
v případě  .
.
Obdobně pro funkci 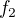 , která je zúžením funkce
, která je zúžením funkce  na interval
na interval ![kopírovat do textarea $(-\infty,\,0]$](/mathtex/77/776bf31783697950b240ab2924018d49.gif) - inversní funkcí k ní je buďto
- inversní funkcí k ní je buďto ,
,  v případě
v případě  nebo
nebo ,
,  v případě
v případě  ,
,
tedy opačně než u funkce 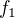 .
.
EDIT: Určitého technického zjednodušení bychom mohli dosáhnout vyjádřením  , kde
, kde  .
.
Offline
#16 10. 01. 2011 18:20
Re: Inverzní fce
↑ Rumburak: dekuji mnohokrat, lepsi vysvetleni jsem nemohl dostat... toto mi vzdy delalo problemy, musim to vzit pomalu krok po kroku... jsem dluznikem...
Offline

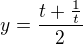


 s tim ze posledni logaritmus by sel jeste rozepsat....?
s tim ze posledni logaritmus by sel jeste rozepsat....?
 vypadal muj krok pred tim nesmyslem... skvele... dekuji mnohkrat vsem a smekam
vypadal muj krok pred tim nesmyslem... skvele... dekuji mnohkrat vsem a smekam